PE 3 - Cubes | LR - Cubes
Join our Telegram Group for CAT Preparation.
Answer the following questions based on the information given below.
The faces of the cuboid are painted with three different colours - black, red, and yellow such that each colour is painted on at least one face. Now 4, 5 and 6 cuts are made in three different directions.
What is the maximum possible number of smaller pieces that have only black on their faces?
Answer: 90
Join our Telegram Group for CAT Preparation.
Explanation :
Maximum number of black pieces will be obtained when maximum faces are painted black and maximum cuts are made on faces painted black.

i.e., 2 opposite faces with 5 and 6 cuts will be painted black and two other opposite faces with 4 and 6 cuts are painted black. Rest two faces are painted yellow and red.
The maximum number of pieces with only black color will be = 2(4 × 5) [front and back faces] + 2(3 × 5) [right and left faces] + 4 × 5 [edges] = 40 + 30 + 20 = 90.
Hence, 90.
Workspace:
What is the maximum possible number of smaller pieces that have only black and yellow painted on their faces?
Answer: 32
Join our Telegram Group for CAT Preparation.
Explanation :
Only black and yellow pieces will come from edge, hence maximum numberer of edges should have black and yellow.
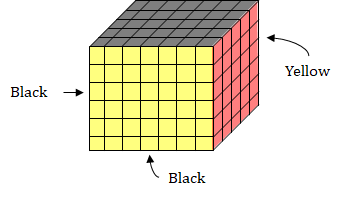
Out of the front 4 edges, 3 edges will give 6 + 4 + 6 = 16 such pieces each.
Out of the back 4 edges, 3 edges will give 6 + 4 + 6 = 16 such pieces each.
∴ Total required pieces = 16 + 16 = 32.
Hence, 32.
Workspace:
What is the maximum number of smaller pieces with three colors painted on them, respectively?
Answer: 8
Join our Telegram Group for CAT Preparation.
Explanation :
If we paint each color on two opposite faces, all 8 corners will have 3 sides painted with 3 different colors.
Hence, 8.
Workspace:
Answer the following questions based on the information given below.
A cube is painted using 3 different colors Red, Yellow and Green on three, two and one face respectively, such that no two faces with same color are opposite each other. The cube is then cut into 125 smaller but identical cubes.
How many smaller cubes have exactly 2 colors on them?
Answer: 29
Join our Telegram Group for CAT Preparation.
Explanation :

Let us first consider middle of the edges:
The top 4 edges, will give 3 such cubes each, hence total 12 such cubes.
Out of bottom 4 edges, only 2 edges will give 3 such cubes each, hence 6 such cubes.
Out of vertical 4 edges, only 2 edges will give 3 such cubes each, hence 6 such cubes.
Now, corners:
Out of 8 corners, 5 corners will have exactly 2 colors on them.
∴ Total number of cubes with exactly 2 colors on them = 12 + 6 + 6 + 5 = 29.
Hence, 29.
Workspace:
How many smaller cubes have Red & Green but not Yellow on them?
Answer: 7
Join our Telegram Group for CAT Preparation.
Explanation :
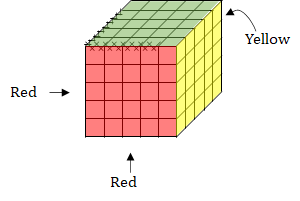
Such cubes are marked in the figure.
There are 3 + 1 + 3 = 7 such cubes which have red and green but not yellow on them.
Hence, 7.
Workspace:
How many smaller cubes do not have Red on them?
Answer: 64
Join our Telegram Group for CAT Preparation.
Explanation :
The number of cubes with red on them =
5 × 5 = 25 (on front face)
5 × 4 = 20 (on bottom face)
4 × 4 = 16 (on left face)
∴ Total = 25 + 20 + 16 = 61 cubes.
∴ The number of cubes not having red on them = 125 – 61 = 64
Hence, 64.
Workspace:
How many smaller cubes have exactly one color on them?
Answer: 67
Join our Telegram Group for CAT Preparation.
Explanation :
Center of Faces:
Each of the 6 faces will give 3 × 3 = 9 middle cubes with exactly one color on them. Hence, total 6 × 9 = 54 such cubes.
Middle of Edges:
Three red edges and one yellow edge will give 3 such cubes, hence total 12 such cubes.
Corners:
One red corner will give 1 such cube.
∴ Total number of cubes with exactly one color on them = 54 + 12 + 1 = 67
Hence, 67.
Workspace:
Answer the following questions based on the information given below.
A cube is painted using 3 different colors such that each color is painted on exactly two opposite faces of the cube. Now this cube is cut into 210 smaller but identical pieces using minimum number of cuts.
How many pieces have exactly two colors on them?
Answer: 48
Join our Telegram Group for CAT Preparation.
Explanation :
The number of cuts will be minimum when the number of cuts made along 3 axes are as equal as possible.
210 = 5 × 6 × 7
∴ Number of pieces along three axes will be 5, 6 and 7.
∴ Number of cuts along three axes will be 4, 5 and 6.
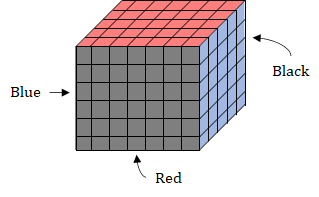
We will cubes with get exactly 2 colors on them from middle of the edges.
There are 4 edges each with 5 cubes, 4 cubes and 3 cubes.
∴ Total such cubes = 4 × (5 + 4 +3) = 48.
Hence, 48.
Workspace:
How many pieces have exactly one color on them?
Answer: 94
Join our Telegram Group for CAT Preparation.
Explanation :
Number of cubes with exactly 1 color on them will be from middle of the faces.
There are 2 faces each with 4 × 5 = 20 cubes, 4 × 3 = 12 cubes and 3 × 5 = 15 cubes.
∴ Total such cubes = 2 × (20 + 12 + 15) = 94.
Hence, 94.
Workspace:
A cube such that the number of colors on it is less than the number of its painted faces, is called an Ego-Cube. How many of the smaller cubes are Ego-Cubes?
Answer: 0
Join our Telegram Group for CAT Preparation.
Explanation :
The cube should be such that the number of colors on it should be less than the number of its painted faces.
This is possible when more than 1 face of the cube is painted with same color.
Here, we do not have cube with same color on more than 1 face.
Hence, 0.
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report