CRE 1 - Mixtures | Arithmetic - Mixture, Alligation, Removal & Replacement
Join our Telegram Group for CAT Preparation.
Akanksha bought 5 kg sugar at Rs. 70/kg. At another shop, she bought 10 kg sugar at Rs 55/kg. What is the average price (in Rs) per kg of the sugar that Akanksha bought?
Answer: 60
Join our Telegram Group for CAT Preparation.
Explanation :
Total quantity bought by Akanksha = 5 + 10 = 15 kgs
Total cost = 5 × 70 + 10 × 55 = 900
Average Price = = 60.
Therefore, average price = Rs. 60/-
Hence, 60.
Workspace:
In a mixture of 130 litres of milk and water mixed in the ratio of 10 : 3, how much water must be added to it so that the ratio of milk and water may be 8 : 5?
- (a)
32.5
- (b)
35
- (c)
32
- (d)
None of these
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
Water in 130 lit. mix = =30 lit
∴ milk = 130 - 30 = 100 lit
Let x liters of water is added now such that milk water ratio becomes 8 : 5.
Now,
⇒ x = 32.5 lit.
Hence, option (a).
Workspace:
64 litres of a mixture, which has milk and water in the ratio 5 : 3 is mixed with 36 litres of a mixture, which has water and milk in the ratio 1 : 2. What is the percentage of water in the resultant mixture?
Answer: 36
Join our Telegram Group for CAT Preparation.
Explanation :
Solution 1:
64 litres of a mixture, which has milk and water in the ratio 5 : 3
Quantity of milk = × 64 = 40 litres
Quantity of water = × 64 = 24 litres
Solution 2:
36 litres of a mixture, which has milk and water in the ratio 2 : 1
Quantity of milk = × 36 = 24 litres
Quantity of water = × 36 = 12 litres
Total quantity of milk in the final mixture = 40 + 24 = 64 liters
Total quantity of water in the final mixture = 24 + 12 = 36 liters
∴ Percentage of water = × 100% = 36%
Hence, 36.
Workspace:
A merchant has 16 kg of sugar, part of which he sells at 10% profit and the rest at 6% profit. He gains 7% on the whole. How much is sold at 6%?
- (a)
4 kg
- (b)
10 kg
- (c)
12 kg
- (d)
8 kg
- (e)
None of these
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Let the quantity sold at 6% is x kgs and at 10% profit is (16 - x) kgs.
⇒ Overall profit = 7% =
⇒ 112 = 6x + 160 – 10x
⇒ x = 12 kgs.
Alternately,

=
Quantity sold at 6% = × 16 = 12 kgs
Hence, option (c).
Workspace:
Rs. 2000 is lent out in two parts, one at 5% simple interest and the other at 7% simple interest. The yearly income is Rs. 130. Find the sum lent at 7%.
- (a)
500
- (b)
1500
- (c)
1600
- (d)
400
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
The overall rate of interest = = 6.5%
Let the amount lent at 7% be x and at 5% be (2000 - x).
⇒ 6.5 =
⇒ 13000 = (2000 - x) × 5 + x × 7
⇒ 3000 = 2x
⇒ x = 1500.
Alternately,
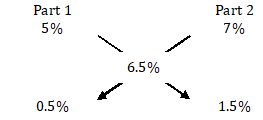
= =
⇒ Amount lent at 7% = × 2000 = Rs. 1500.
Hence, option (b).
Workspace:
The proportion of wine and water in 3 samples is 1 : 2, 2 : 3 and 3 : 5. A mixture comprising of equal quantities of all 3 samples is made. The proportion of wine and water in the mixture is:
- (a)
1 : 2
- (b)
1 : 5
- (c)
61 : 99
- (d)
133 : 227
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Proportion of wine in 3 samples is
Proportion of water in 3 samples is
Since equal quantities are taken, let 1 liter of each is mixed.
Total quantity of wine is =
Total quantity of water is =
∴ Proportion of wine and water in the solution is = 133 : 227.
Alternately,
Proportion of wine in 3 samples is
Proportion of water in 3 samples is
Since equal quantities are taken, let 120 liter of each is mixed. (We’ve chosen 120 liters since it is divisible by the denominators of all the fractions i.e. LCM(3, 5 and 8) = 120)
Total quantity of wine is = 40 + 48 + 45 = 133.
Total quantity of water is = 80 + 72 + 75 = 227.
∴ Proportion of wine and water in the solution is = 133 : 227.
Hence, option (d).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report