Concept: Quandrilaterals & Polygons
CONTENTS
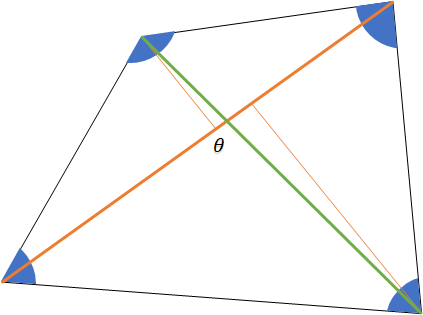
Sum of all the angles of a quadrilateral is 360°
Sum of all the exterior angles of a quadrilateral is 360°
Area = ½ × (one diagonal) × (Sum of heights on this diagonal)
Area = ½ × d1d2 × 𝑆𝑖𝑛𝜃
Sum of the 4 sides > Sum of the 2 diagonals
Any side < Sum of the remaining 3 sides
Any side > Least difference of any of the remaining 2 sides
General Properties of Parallelograms
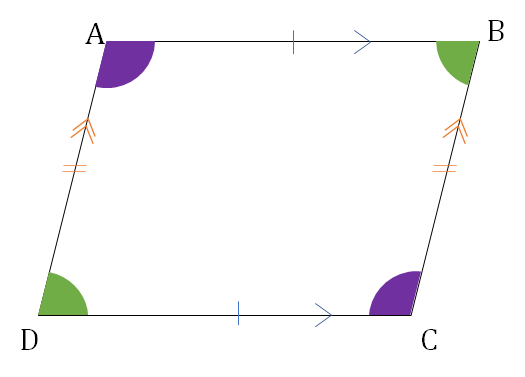
Opposite sides are parallel and equal
Opposite angles are equal
Area = base × height
Diagonals bisect each other
Adjacent angles are supplementary
Each diagonal divides the ||gm in two congruent triangles.
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
Parallelogram with same base and between same parallel lines will have same area
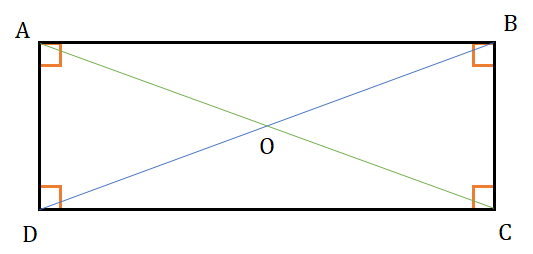
All properties of a ||gm.
All angles are equal to 90°.
Both diagonals are equal and bisect each other.
- AC = BD =
- OA = OB = OC = OD
If P is a point inside the rectangle, then
Area = l × b
Figure formed by joining the midpoints is a rhombus.
Rectangle has a circumcircle but not incircle.
PA2 + PC2 = PB2 + PD2
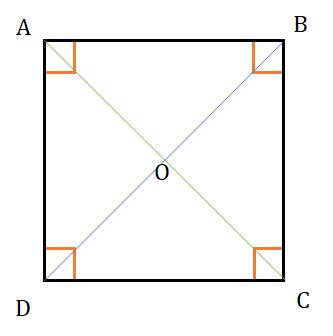
All properties of a rectangle.
Both diagonals are equal (a√2) and bisect each other at 90°.
Diagonals bisect the vertex angles.
Area = a2
Figure formed by joining the midpoints is a square.
Square has both circumcircle as well as a incircle.
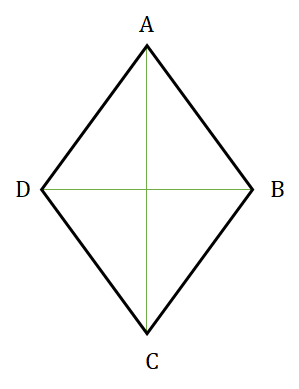
All properties of a ||gm.
Diagonals are not necessarily equal but bisect each other at 90°
Diagonals bisect the vertex angles.
d12 + d22 = 4a2
Area = ½ × d1d2
Figure formed by joining the midpoints is a rectangle.
Rhombus has an incircle but no circumcircle.

Kite is not a parallelogram.
2 pair of Adjacent sides are equal.
Here, AD = AB and CD = CB
Bigger diagonal bisects the smaller diagonal at 90°.
Area = ½ × d1d2
Opposite angles along the smaller diagonal are equal.
Here, ∠D = ∠B
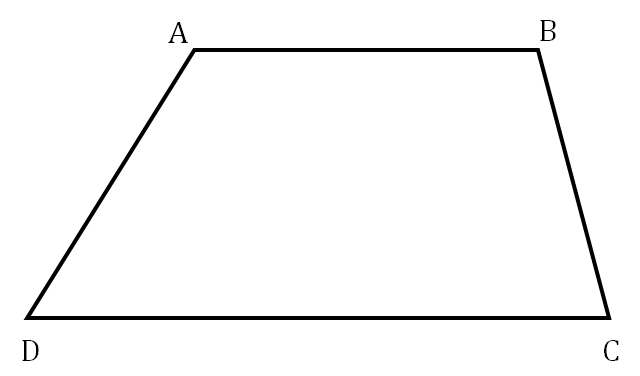
One pair of opposite sides (bases) is parallel.
Area = ½ × ℎ𝑒𝑖𝑔ℎ𝑡 × (𝑠𝑢𝑚 𝑜𝑓 𝑏𝑎𝑠𝑒𝑠)
The length of a line dividing the oblique sides in the ratio a : b is given by
Diagonals divide the median in the ratio of length of parallel sides
× CD + × AB
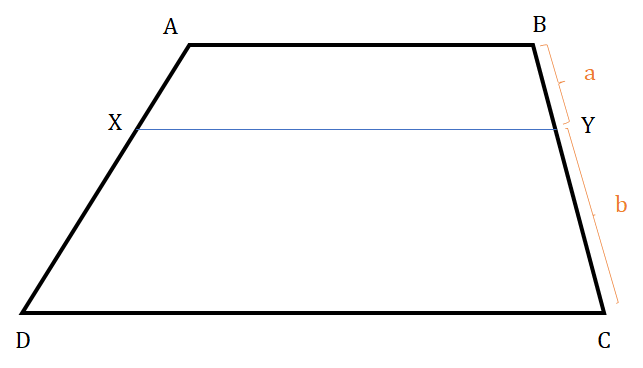
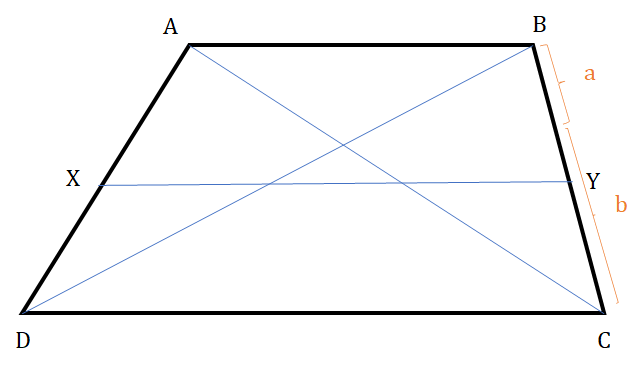
Isosceles Trapezium
If oblique sides are equal, it is called an isosceles trapezium.
If a trapezium is inscribed inside a circle, it will always be an isosceles trapezium, i.e. its non−parallel sides will be equal
AD = BC and ∠D = ∠C
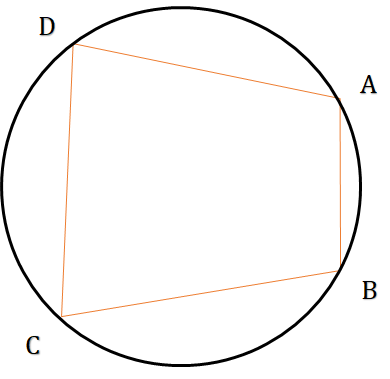
A quadrilateral whose all 4 vertices lie on the same circle is called a cyclic quadrilateral. The sum of any two opposite angles of a cyclic quadrilateral is 180°.
Area of a cyclic quadrilateral =
where s = semiperimeter =

A polygon is a closed figure bounded by three or more straight lines, known as sides. It has as many vertices as the number of sides, with no three of them collinear.
A line joining two non−adjacent vertices is known as the diagonal.
No. of diagonals in a ‘n’ sided polygon:
Sum of internal angles of a ′n′ sided polygon: (n - 2)π
Sum of exterior angles of a ′n′ sided polygon: 2π
A convex polygon has all angles < 180°.
A concave polygon has at least one angle > 180°.
Measure of each interior angle:
Measure of each exterior angle:
Area of a regular ′n′ sided polygon: n × (area of smaller triangle)
Inradius of a n sided regular polygon = cot
Circumradius of a n sided regular polygon: cosec
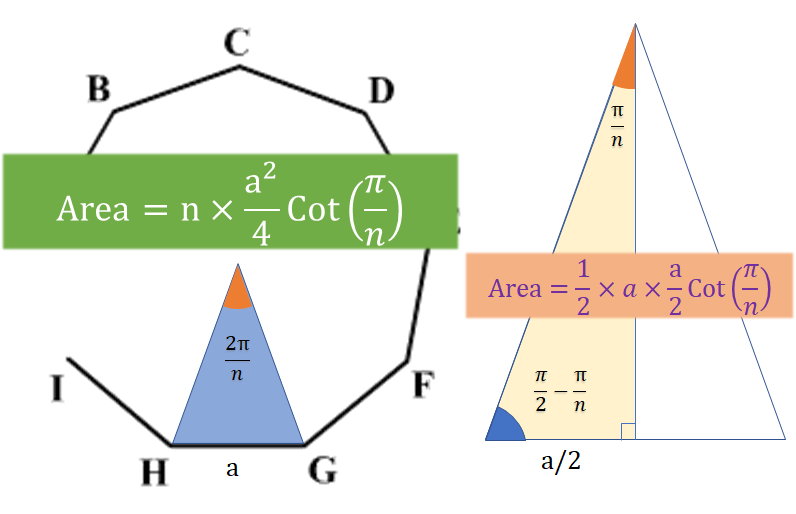
i.e., n × Cot

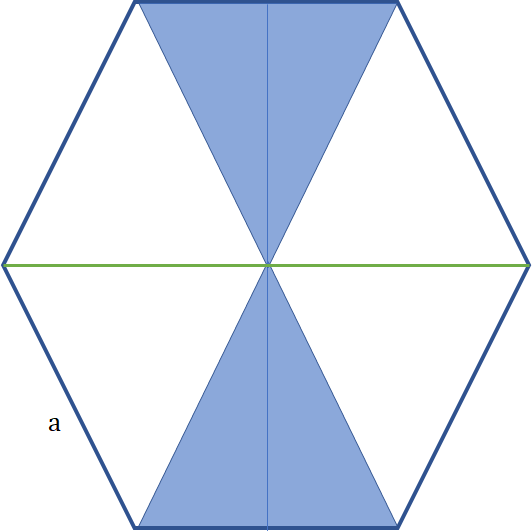
Height of a regular hexagon: a√3
Distance between opposite vertices: 2a
Area of a regular hexagon: 6 ×

- For a fixed perimeter, the area of a polygon with higher number of sides will always be more than the area of a polygon with lesser number of sides.
- For any fixed area, the perimeter of a regular polygon with lesser number of sides will always be more than that of a regular polygon with a greater number of sides.
- If the circumference of a circle is the same as the perimeter of a regular polygon, then the area of the circle will always be more than the area of the polygon.