CRE 6 - Higher Degree Polynomials | Algebra - Quadratic Equations

Answer: Option C

Join our Telegram Group for CAT/MBA Preparation.

Explanation :

We know any equation whose roots are α, β, γ, ... and so on can be formed as (x - α) × (x - β) × (x - γ) × ... = 0

∴ The required equation is (x - 1)(x - 2)(x - 3) = 0

⇒ x³ - (1 + 2 + 3)x² + (1 × 2 + 2 × 3 + 3 × 1)x - 1 × 2 × 3 = 0

⇒ x³ - 6x² + 11x - 6 = 0

Hence, option (c).

Answer: Option C

Join our Telegram Group for CAT/MBA Preparation.

Explanation :

The given equation is x³ – 2x² – x + 2 = 0

∴ The sum of the roots = -b/a = -(-2)/1 = 2

and, Product of the roots = -c/a = -(2/1) = -2

Now either we can check for options or figure out the roots using hit and trial such that their sum is 2 and their product is -2.

Such numbers are -1, 1 and 2.

Alternately,
The sum of the coefficients of the given equation is 0, hence one of the roots of the equation will be 1.

∴ (x - 1) is a factor of x³ – 2x² – x + 2

When x³ – 2x² – x + 2 is divided by (x - 1), quotient is x² – x - 2

Now, we need to solve for x² – x - 2 = 0

⇒ (x - 2)(x + 1) = 0

⇒ x = -1 or 2

∴ x = -1 or 1 or 2

Hence, option (c).

Answer: Option A

Join our Telegram Group for CAT/MBA Preparation.

Explanation :

Givne, 2x³ - 3x² - 6x + 4 = 0

Now, $\frac{1}{\mathrm{\alpha }}$ + $\frac{1}{\mathrm{\beta }}$ + $\frac{1}{\mathrm{\gamma }}$ = $\frac{\mathrm{\alpha \beta }+\mathrm{\beta \gamma }+\mathrm{\alpha \gamma }}{\mathrm{\alpha \beta \gamma }}$

In the given equation, αβγ = -(4/2) = -2, and

αβ + βγ + γα = (-6/2) = -3

∴ $\frac{1}{\mathrm{\alpha }}$ + $\frac{1}{\mathrm{\beta }}$ + $\frac{1}{\mathrm{\gamma }}$ = $\frac{\mathrm{\alpha \beta }+\mathrm{\beta \gamma }+\mathrm{\alpha \gamma }}{\mathrm{\alpha \beta \gamma }}$ = $\frac{-3}{-2}$ = $\frac{3}{2}$

Hence, option (a).

Answer: Option A

Join our Telegram Group for CAT/MBA Preparation.

Explanation :

Step 1: 
​​​​​​​

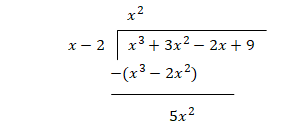
Step 2:

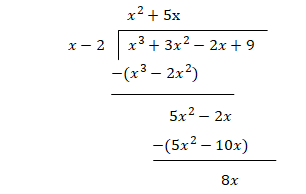
Step 3:
​​​​​​​​​​​​​​

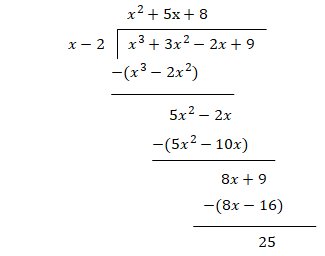
The remainder is 25.

Alternately,
If we need to find the remainder when f(x) is divided by (ax + b) 

We first equate ax + b with 0, i.e., ax + b = 0 hence, x = -b/a

Now, remainder of f(x) when divided by (ax + b) = f(-b/a).

Here, f(x) = 𝑥³ + 3𝑥² − 2𝑥 + 9, its remainder when divided by x - 2.

x - 2 = 0, hence, x = 2

∴ The remainder here is f(2) = 2³ + 3(2)² − 2(2) + 9 = 8 + 12 - 4 + 9 = 25

Hence, option (a).