Algebra - Simple Equations - Previous Year CAT/MBA Questions
The best way to prepare for Algebra - Simple Equations is by going through the previous year Algebra - Simple Equations CAT questions. Here we bring you all previous year Algebra - Simple Equations CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Algebra - Simple Equations CAT questions.
Join our Telegram Group for CAT Preparation.
Manu earns ₹4000 per month and wants to save an average of ₹550 per month in a year. In the first nine months, his monthly expense was ₹3500, and he foresees that, tenth month onward, his monthly expense will increase to ₹3700. In order to meet his yearly savings target, his monthly earnings, in rupees, from the tenth month onward should be:
- (a)
4400
- (b)
4300
- (c)
4200
- (d)
4350
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
Monthly savings of Manu = Rs. 550
⇒ Yearly savings of Manu = 12 × 550 = Rs. 6,600
Total expense of Manu for the first 9 months = 9 × 3500 = Rs. 31,500
Total expense of Manu for the last 3 months = 3 × 3700 = 11,100
⇒ Yearly expense of Manu = 11,100 + 31,500 = Rs. 42,600
Monthly income of Manu = Rs. 4,000
⇒ Income of Manu for first 9 months = 9 × 4000 = Rs. 36,000
⇒ Manu’s income for last 3 months = 42,600 + 6,600 – 36,000 = Rs. 13,200
⇒ Monthly income of Manu for last 3 months = = Rs. 4,400
Hence, option (a).
Workspace:
Five students, including Amit, appear for an examination in which possible marks are integers between 0 and 50, both inclusive. The average marks for all the students is 38 and exactly three students got more than 32. If no two students got the same marks and Amit got the least marks among the five students, then the difference between the highest and lowest possible marks of Amit is
- (a)
24
- (b)
20
- (c)
21
- (d)
22
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Total marks of all 5 students = 5 × 38 = 190
Case 1: Least marks of Amit.
To minimize Amit’s marks we should maximize the marks of other 4 students.
⇒ 3 students get more than 32, hence their maximum marks can be 48, 49 and 50. [Marks are distinct]
2 students (including Amit) scored less than or equal to 32.
⇒ Maximum marks of 2nd student can be 32
∴ Sum of marks of these 4 students = 32 + 48 + 49 + 50 = 179
⇒ Least marks of Amit = 190 – 179 = 11
Case 2: Maximum marks of Amit.
Since Amit and one other student scored less than or equal to 32 marks, maximum marks Amit can score is 31. [Amit scored least and all scores are distinct.]
∴ Difference between highest and least score of Amit = 31 – 11 = 20
Hence, option (b).
Workspace:
In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is:
Answer: 24
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the number of correct, wrong and un-attempted questions be c, w and u respectively.
Since u > c + w
⇒ u > 75 - u
⇒ u > 37.5
∴ Least possible value of u is 38
⇒ c + w + u = 75 …(1)
⇒ 3c – w + u = 97 …(2)
(2) + (1)
⇒ 4c + 2u = 172
⇒ 2c + u = 86
⇒ 2c = 86 - u
c will be greatest when u is least i.e., u = 38
⇒ 2c = 86 - 38 = 48
⇒ c = 24
∴ Maximum value c can take is 24.
Hence, 24.
Workspace:
A donation box can receive only cheques of ₹100, ₹250, and ₹500. On one good day, the donation box was found to contain exactly 100 cheques amounting to a total sum of ₹15250. Then, the maximum possible number of cheques of ₹500 that the donation box may have contained, is
Answer: 12
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the number of 100, 250 and 500 notes be a, b and c respectively.
⇒ a + b + c = 100 …(1)
⇒ 100a + 250b + 500c = 15250
⇒ 2a + 5b + 10c = 305 …(2)
(2) – 2 × (1)
⇒ 3b + 8c = 105
⇒ c = = = 13 +
c will be maximum when b is minimum. The least value b can take such that c is integer is 3.
∴ c = 13 + = 12
Hence, 12.
Workspace:
A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is
- (a)
13
- (b)
12
- (c)
11
- (d)
10
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the cost of each apple be ‘a’, each orange be ‘o’ and each mango be ‘m’.
∴ 2a + 4o + 6m = a + 4o + 8m = 8o + 7m
⇒ 2a + 4o + 6m = 8o + 7m
⇒ 4o + m = 2a …(1)
Also, a + 4o + 8m = 8o + 7m
⇒ 4o – m = a …(2)
Solving (1) and (2) we get
8o = 3a and m = a/2
∴ Value of each basked in terms of mangoes
= 2a + 4o + 6m
= 4m + 3a/2 + 6m
= 10m + 3/2 × 2m
= 10m + 3m
= 13m
∴ Value of each basket is same as value of 13 mangoes.
Hence, option (a).
Workspace:
How many three-digit numbers are greater than 100 and increase by 198 when the three digits are arranged in the reverse order?
Answer: 70
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the required three-digit number be ‘abc’.
According to the question:
‘abc’ + 198 = ‘cba’
⇒ 100a + 10b + c + 198 = 100c + 10b + a
⇒ 99c – 99a = 198
⇒ c – a = 2
∴ Value of (c, a) can be (9, 7) or (8, 6) or (7, 5) or (6, 4) or (5, 3) or (4, 2) or (3, 1) i.e., total 7 values.
For each of these 7 values of c and a, b can taken any of the 10 values from 0 to 9.
∴ Total such possible numbers = 7 × 10 = 70.
Hence, 70.
Workspace:
A box has 450 balls, each either white or black, there being as many metallic white balls as metallic black balls. If 40% of the white balls and 50% of the black balls are metallic, then the number of non-metallic balls in the box is
Answer: 250
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let total number of black balls be 100b and total number of white balls be 100w.
∴ 100w + 100b = 450
⇒ w + b = 4.5 …(1)
According to the question.
Number of metallic balls:
White metallic = 40% of 100w = 40w
Black metallic = 50% of 100b = 50b
Now, 40w = 50b
⇒ w = 1.25b …(2)
From (1) and (2)
1.25b + b = 4.5
⇒ b = 2 and w – 2.5
∴ Number of non-metallic white balls = 60% of 100w = 150
and, number of non-metallic black balls = 50% of 100b = 100
∴ Total number of non-metallic balls = 150 + 100 = 250
Hence, 250.
Workspace:
A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
Answer: 62
Join our Telegram Group for CAT Preparation.
Text Explanation :
Giving chocolates to 5th child:
Let the man be left with x chocolates after 4th child.
Now he gives half of x i.e., x/2 chocolates to 5th child. Hence, he will be left with x/2 chocolates.
The man again gives 1 chocolate to 5th child and is now left with no chocolates.
∴ x/2 – 1 = 0
⇒ x = 2
Giving chocolates to 4th child:
Now, let the man be left with y chocolates after 3rd child.
Now he gives half of y i.e., y/2 chocolates to 4th child. Hence, he will be left with y/2 chocolates.
The man again gives 1 chocolate to 4th child and is now left with 2 chocolates.
∴ y/2 – 1 = 2
⇒ y = 6
Giving chocolates to 3rd child:
Now, let the man be left with z chocolates after 2nd child.
∴ z/2 – 1 = 6
⇒ y = 14
Giving chocolates to 2nd child:
Now, let the man be left with a chocolates after 1st child.
∴ a/2 – 1 = 14
⇒ y = 30
Giving chocolates to 1st child:
Now, let the man have c chocolates in the beginning.
∴ c/2 – 1 = 30
⇒ y = 62
Hence, 62.
Workspace:
Aron bought some pencils and sharpeners. Spending the same amount of money as Aron, Aditya bought twice as many pencils and 10 less sharpeners. If the cost of one sharpener is ₹ 2 more than the cost of a pencil, then the minimum possible number of pencils bought by Aron and Aditya together is
- (a)
27
- (b)
36
- (c)
33
- (d)
30
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the price of a pencil = x and that of a sharpener = x + 2.
Suppose Aron bought p pencils and s sharpeners. Aditya buys 2x pencils and s – 10 sharpeners.
∴ px + s(x + 2) = 2px + (s – 10)(x + 2)
⇒ px + sx + 2s = 2px + sx + 2s – 10x – 20
⇒ 20 = px – 10x
⇒ x(p – 10) = 20
Here, the least value of p can be 11.
∴ Aron and Aditya together bought 3p pencils and least value of 3p = 3 × 11 = 33.
Hence, option (c).
Workspace:
Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if
- (a)
|k| = 2
- (b)
k = 2
- (c)
|k| ≠ 2
- (d)
k ≠ 2
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
For 2 equations a1x + b1y = c1 and a2x + b2y = c2 to have a unique solution, the condition is: .
∴
⇒ k2 = 4
⇒ k = ±2 or |k| ≠ 2.
Hence, option (c).
Workspace:
In a six-digit number, the sixth, that is, the rightmost, digit is the sum of the first three digits, the fifth digit is the sum of first two digits, the third digit is equal to the first digit, the second digit is twice the first digit and the fourth digit is the sum of fifth and sixth digits. Then, the largest possible value of the fourth digit is
Answer: 7
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the first digit be = a
Second digit = Twice of first digit = 2a
Third digit = First digit = a
Fifth digit = Sum of first two digits = a + 2a = 3a
Sixth digit = Sum of first three digits = a + 2a + a = 4a
Fourth digit = Sum of fifth and sixth digit = 3a + 4a = 7a
Largest possible value of fourth digit = 7 (it has to be a single digit integer)
Hence, 7.
Workspace:
A shop stores x kg of rice. The first customer buys half this amount plus half a kg of rice. The second customer buys half the remaining amount plus half a kg of rice. Then the third customer also buys half the remaining amount plus half a kg of rice. Thereafter, no rice is left in the shop. Which of the following best describes the value of x?
- (a)
2 ≤ x ≤ 6
- (b)
5 ≤ x ≤ 8
- (c)
9 ≤ x ≤ 12
- (d)
11 ≤ x ≤ 14
- (e)
13 ≤ x ≤ 18
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
The initial quantity of rice is x kg.
The first customer buys half the total rice in the store, and another half kg.
∴ Rice purchased by the first customer =
∴ Remaining rice =
Now, the second customer buys half of this, and another half kg.
∴ Rice purchased by the second customer =
∴ Remaining rice =
Now, the third customer buys half the remaining rice, and another half kg.
∴ Rice purchased by the third customer =
Since after this purchase, there is no rice left in the store, we conclude that:
∴ x = 7
Alternately,
If the shopkeeper had x kg rice before a customer comes, the amount of rice left after every time a customer buys half the amount of rice + half a kg more =
For 3rd customer.
Now, = 0 [No rice is left after third customer]
⇒ x = 1 kg.
Now, the shopkeeper had 1 kg rice when 3rd customer came, hence after 2nd customer left he had 1 kg of rice.
For 2nd customer.
= 1
⇒ x = 3 kg.
Now, the shopkeeper had 3 kg rice when 2nd customer came, hence after 1st customer left he had 3 kg of rice.
For 1st customer.
= 3
⇒ x = 7 kg.
Now, the shopkeeper had 7 kg rice when 1st customer came.
Hence, option (b).
Workspace:
Suppose you have a currency, named Miso, in three denominations: 1 Miso, 10 Misos and 50 Misos. In how many ways can you pay a bill of 107 Misos?
- (a)
17
- (b)
16
- (c)
18
- (d)
15
- (e)
19
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let number of 50, 10 and 1 miso notes used is x, y and z respectively.
⇒ 50x + 10y + z = 107
Now, since x, y and z are whole numbers x can take only three values i.e., 0, 1 and 2.
Case 1: x = 0
⇒ 10y + z = 107
⇒ y can take values from 0 till 10 i.e., 11 values
∴ 11 ways to pay bill of 107 misos.
Case 2: x = 1
⇒ 10y + z = 57
⇒ y can take values from 0 till 5 i.e., 6 values
∴ 6 ways to pay bill of 107 misos.
Case 3: x = 2
⇒ 10y + z = 7
⇒ y can take only 1 value i.e., 0
∴ 1 way to pay bill of 107 misos.
⇒ Total ways the bill can be paid = 11 + 6 + 1 = 18 ways,
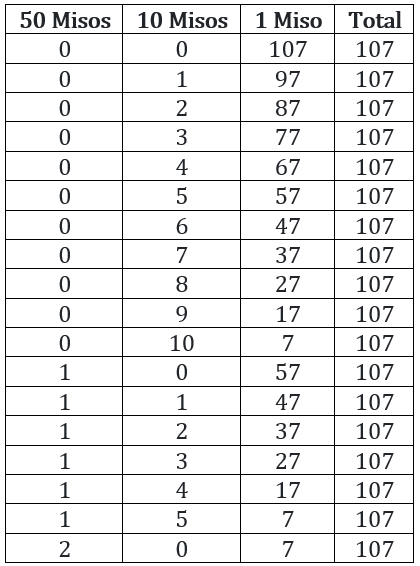
The bill can be paid in 18 ways as shown in the above table.
Hence, option (c).
Workspace:
A confused bank teller transposed the rupees and paise when he cashed a cheque for Shailaja, giving her rupees instead of paise and paise instead of rupees. After buying a toffee for 50 paise, Shailaja noticed that she was left with exactly three times as much as the amount on the cheque. Which of the following is a valid statement about the cheque amount?
- (a)
Over Rupees 13 but less than Rupees 14
- (b)
Over Rupees 7 but less than Rupees 8
- (c)
Over Rupees 22 but less than Rupees 23
- (d)
Over Rupees 18 but less than Rupees 19
- (e)
Over Rupees 4 but less than Rupees 5
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the amount on Shailaja’s cheque be Rs. x and paise y = (100x + y) paise (x and y are positive integers)
The teller gives her (100y + x) paise.
Now, 100y + x – 50 = 3(100x + y)
∴ 97y – 299x = 50
∴ y = (50 + 299x)/97 = [50 + 8x + 291x]/97 = [(50 + 8x)/97] + 3x
Now as y is an integer, (50 + 8x) has to be a multiple of 97 with x, y ≤ 99
50 + 8x = 97k (k is an integer)
∴ k = 2, 10, 18…
∴ x = 18, 115, 212…
∴ x = 18 is the only possible value.
This implies that y = 5
∴ The amount on Shailaja’s cheque is over Rs. 18 but less than Rs. 19.
Hence, option (d).
Workspace:
The number of solutions of the equation 2x + y = 40 where both x and y are positive integers and x ≤ y is:
- (a)
7
- (b)
13
- (c)
14
- (d)
18
- (e)
20
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
2x + y = 40
∴ y = 40 – 2x
x and y are positive integers and x ≤ y
If x = 1, y = 38
x = 2, y = 36
x = 3, y = 34
.
.
.
x = 12, y =16
x = 13, y = 14
x = 14, y = 12
∴ For x > 13, y ≤ x
∴ There are 13 solutions to the given equation.
Hence, option (b).
Workspace:
When you reverse the digits of the number 13, the number increases by 18. How many other two digit numbers increase by 18 when their digits are reversed?
- (a)
5
- (b)
6
- (c)
7
- (d)
8
- (e)
10
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let 10x + y be a two digit number, where x and y are positive single digit integers and x > 0.
Its reverse = 10y + x
Now, |10y + x – 10x – y| = 18
∴ 9 |y – x| = 18
∴ |y – x| = 2
Thus y and x can be (1, 3), (2, 4), (3, 5), (4, 6), (5, 7), (6, 8) and (7, 9)
∴ Other than 13, there are 6 such numbers.
Hence, option (b).
Workspace:
A telecom service provider engages male and female operators for answering 1000 calls per day. A male operator can handle 40 calls per day whereas a female operator can handle 50 calls per day. The male and the female operators get a fixed wage of Rs. 250 and Rs. 300 per day respectively. In addition, a male operator gets Rs. 15 per call he answers and a female operator gets Rs. 10 per call she answers. To minimize the total cost, how many male operators should the service provider employ assuming he has to employ more than 7 of the 12 female operators available for the job?
- (a)
15
- (b)
14
- (c)
12
- (d)
10
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let us calculate the cost per call for a male and a female.
Male: A male can make 40 calls/day.
Total cost = 250 + 15 × 40 = 850
∴ Cost/call for a male = 850/40 = Rs. 21.25
Female: A female can make 50 calls/day.
Total cost = 300 + 10 × 50 = 800
∴ Cost/call for a female = 800/50 = Rs. 16
Hence, it could be cost effective to employ as many females as possible.
We have maximum 12 females who can make 12 × 50 = 600 calls/day.
Remaining (1000 - 600 =) 400 calls should be made by males.
∴ Number of males to be employed = 400/40 = 10 males.
Alternately,
Let x females and y males be employed.
As the total number of calls to be answered = 1000 and males and females can handle 40 and 50 calls respectively everyday
50x + 40y = 1000
40y = 1000 – 50x
∴ y = 25 – x – x/4
As 7 < x ≤ 12, x can be 8 or 12.
If x = 8, y = 15 and if x = 12, y = 10
The total cost of employing x females and y males
= 300x + 250y + (50 × 10 × x) + (40 × 15 × y)
= 800x + 850y
If x = 8 and y = 15, cost = Rs. 19,150
If x = 12 and y = 10, cost = Rs. 18,100
Thus, cost is minimized when the number of male operators is 10.
Hence, option (d).
Workspace:

In the adjoining figure, chord ED is parallel to the diameter AC of the circle. If ∠CBE = 65°, then what is the value of ∠DEC?
- (a)
35°
- (b)
55°
- (c)
45°
- (d)
25°
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :

m∠EBC = 65°
∴ m∠EOC = 130° (∵ angle subtended by an arc at the centre is twice the angle subtended by the same arc on the circumference)
As AC || ED, m∠OCE = m∠DEC
ΔOEC is an isosceles triangle.
∴ m∠OCE = m∠OEC = (180 – 130)/2 = 25°
∴ m∠DEC = 25°
Hence, option (d).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Ravi spent less than Rs.75 to buy one kilogram each of potato, onion, and gourd. Which one of the three vegetables bought was the costliest?
A. 2 kg potato and 1 kg gourd cost less than 1 kg potato and 2 kg gourd.
B. 1 kg potato and 2 kg onion together cost the same as 1 kg onion and 2 kg gourd.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let one kilogram of potatoes, onions and gourd cost Rs. p, Rs. o and Rs. g respectively. Then p + o + g < 75.
Consider statement A: 2p + g < p + 2g
∴ p < g
But, nothing is known about o.
∴ Statement A is insufficient.
Consider statement B: p + 2o = o + 2g
∴ o + p = 2g
∴ The cost of 1 kg of gourd is the average of the costs of 1 kg potatoes and 1 kg onions.
∴ g is neither the costliest nor the cheapest.
But the costliest vegetable cannot be found.
∴ Statement B is insufficient.
Considering both statements together: p < g and g is the average of p and o
∴ o > g
∴ Onions are the costliest.
Hence, option (c).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Nandini paid for an article using currency notes of denominations Re. l, Rs. 2, Rs. 5, and Rs. 10 using at least one note of each denomination. The total number of five and ten rupee notes used was one more than the total number of one and two rupee notes used. What was the price of the article?
A. Nandini used a total of 13 currency notes.
B. The price of the article was a multiple of Rs. 10.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let Nandini use a, b, c and d notes of denominations 1, 2, 5 and 10 respectively.
Then c + d = a + b + 1 and price of the article = a + 2b + 5c + 10d
Consider statement A: a + b + c + d = 13
∴ 2(a + b) + 1 = 13
∴ a + b = 6, c + d = 7
Price of the article cannot be found from this data.
∴ Statement A is insufficient.
Consider statement B: a + 2b + 5c + 10d = 10k
As a, b, c, d ≥ 1, 10k ≥ 18
∴ k ≥ 2
But, statement B is also insufficient.
Considering both statements together: We know that a + b = 6, c + d = 7 and Price = 10k
When c = 2 and d = 5, Price = a + 2b + 60
When c = 4 and d = 3, Price = a + 2b + 50
Even if we assume that there is only one value of (a, b) such that a + 2b is a multiple of 10, we will still get at least 2 values for the price of the article.
Hence, data is insufficient.
Hence, option (d).
Workspace:
Answer the following question based on the information given below.
A certain perfume is available at a duty-free shop at the Bangkok international airport. It is priced in the Thai currency Baht but other currencies are also acceptable. In particular, the shop accepts Euro and US Dollar at the following rates of exchange:
US Dollar 1 = 41 Bahts and Euro 1 = 46 Bahts
The perfume is priced at 520 Bahts per bottle. After one bottle is purchased, subsequent bottles are available at a discount of 30%. Three friends S, R and M together purchase three bottles of the perfume, agreeing to share the cost equally. R pays 2 Euros. M pays 4 Euros and 27 Thai Bahts and S pays the remaining amount in US Dollars.
How much does R owe to S in Thai Baht?
- (a)
428
- (b)
416
- (c)
334
- (d)
324
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Price of 1st bottle = 520 Bahts
Price of 2nd and 3rd bottles each = (520 × 0.7) = 364 Bahts
∴ Total cost of all three bottles = 1248 Bahts
Cost per person = 416 Bahts
R pays 2 Euros = 2 × 46 = 92 Bahts
M pays 4 Euros and 27 Bahts = 4 × 46 + 27 = 211 Bahts
S pays the remaining amount = 1248 − (92 + 211) = 945 Bahts
∴ R owes 416 − 92 = 324 Bahts to S.
Hence, option (d).
Workspace:
How much does M owe to S in US Dollars?
- (a)
3
- (b)
4
- (c)
5
- (d)
6
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Price of 1st bottle = 520 Bahts
Price of 2nd and 3rd bottles each = (520 × 0.7) = 364 Bahts
∴ Total cost of all three bottles = 1248 Bahts
Cost per person = 416 Bahts
R pays 2 Euros = 2 × 46 = 92 Bahts
M pays 4 Euros and 27 Bahts = 4 × 46 + 27 = 211 Bahts
S pays the remaining amount = 1248 − (92 + 211) = 945 Bahts
M owes = 416 − 211 = 205 Bahts to S
But, 205 Bahts = 205/41 = 5 US Dollars
Hence, option (c).
Workspace:
Which one of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0?
x + 2y − 3z = p
2x + 6y − 11z = q
x − 2y + 7z = r
- (a)
5p − 2q − r = 0
- (b)
5p + 2q + r = 0
- (c)
5p + 2q − r = 0
- (d)
5p − 2q + r = 0
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
On substituting the values of p, q and r in the options we see that the values of p, q and r satisfy only the equation 5p − 2q − r = 0.
Hence, option (a).
Alternatively,
In order to understand this solution we need to have an understanding of a few concepts of higher mathematics like “Rank of a matrix”.
A number p is said to be the rank of a matrix A if
(i) A possesses at least one p-rowed determinant whose value is not zero
(ii) A does not possess any non zero (p + 1) rowed determinant.
In other words, the number of non-zero rows in the row-reduced form of a matrix is called the rank of a matrix.
For example,
Consider the matrix,
Matrix A has only one 3 rowed determinant, namely
The value of this determinant is zero. Hence, the rank of A will be less than 3.
Now we will try to find a 2 rowed non zero determinant.
= 42 - 5.1 = 3 ≠ 0
The fact that every 3 rowed determinant of A is zero and there is at least one 2 rowed determinant of A which is not zero, is generally expressed by saying that the rank of A is 2.
Consider the system of equations,
x + 2y − 3z = p
2x + 6y − 11z = q
x − 2y + 7z = r
The coefficient matrix (whose elements are coefficients of the three unknowns x, y and z) of the system is
And the Augmented matrix is
For the system of equations to possess solutions it is necessary that the rank of the augmented matrix and the rank of the coefficient matrix should be equal.
Let us first find the rank of the coefficient matrix.
We will first find the value of the only 3 rowed determinant of A,
= 1(6 × 7 - 11 × (-2)) - 2(2 × 7 - (-11)1) - 3(2 × (-2) - 6 × 1) = 0
Hence, the rank of the coefficient matrix will be less than 3.
The following is a two-rowed non-zero determinant in the coefficient matrix
= 6 - 4 = 2 ≠ 0
Hence, the rank of the coefficient matrix is 2.
For the system of equations to possess solutions the rank of the augmented matrix should also be 2.
We will first try to simplify the augmented matrix using row operations.
By the row operation R3 → R3 - R1
we reduce the augmented matrix to the equivalent matrix,
(By the row operation R2 → R2 - 2R1)
(By the row operation R3 → R3 - 2R2)
For the augmented matrix to have rank 2 every 3 rowed determinant should be zero.
Hence,
5p − 2q − r = 0
Hence, option (a).
Workspace:
A test has 50 questions. A student scores 1 mark for a correct answer, −1/3 for a wrong answer, and −1/6 for not attempting a question. If the net score of a student is 32, the number of questions answered wrongly by that student cannot be less than
- (a)
6
- (b)
12
- (c)
3
- (d)
9
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let R, W and N be the number of questions with right answers, questions with wrong answers and not attempted questions respectively.
From the conditions given in the question, we have,
R + W + N = 50 … (i)
R − W/3 − N/6 = 32 … (ii)
Solving equations (i) and (ii), we get,
7R − 242 = W
∴ W will be minimum for R = 35, i.e. W = 3
Hence, option (c).
Workspace:
A survey on a sample of 25 new cars being sold at a local auto dealer was conducted to see which of the three popular options- air conditioning, radio and power windows- were already installed. The survey found
- 15 had air conditioning,
- 2 had air conditioning and power windows but no radios,
- 12 had radio,
- 6 had air conditioning and radio, but no power windows,
- 11 had power windows,
- 4 had radio and power windows and
- 3 had all three options.
What is the number of cars that had none of the options?
- (a)
4
- (b)
3
- (c)
1
- (d)
2
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, AC – Air Conditioning, R – Radio and PW – Power Windows
From the given conditions, we have the above Venn diagram.
When we add up all the values in the Venn diagram, we get 23 (15 + 5 + 1 + 2) cars.
∴ 2 (i.e. 25 − 23) cars don’t have any of the three options.
Hence, option (d).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report