Venn Diagram - Previous Year CAT/MBA Questions
The best way to prepare for Venn Diagram is by going through the previous year Venn Diagram CAT questions. Here we bring you all previous year Venn Diagram CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Venn Diagram CAT questions.
Join our Telegram Group for CAT Preparation.
For Venn Diagram questions from LRDI section, please visit this page.
In a class of 100 students, 73 like coffee, 80 like tea and 52 like lemonade. It may be possible that some students do not like any of these three drinks. Then the difference between the maximum and minimum possible number of students who like all the three drinks is
- (a)
52
- (b)
47
- (c)
48
- (d)
53
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Maximum people who can like all three drinks is 52 since least number of people linking a particular drink is 52 for lemonade.
Let the number of students liking
exactly one drink = a
exactly two drinks = b
exactly three drinks = c
exactly no drink = n
⇒ a + 2b + 3c = 73 + 80 + 52 = 205
Even if a = c = 0 and b = 100, a + 2b + 3c = 200
∴ c cannot be zero.
If we shift one student from b to c, the sum will increase by 1.
Hence, to increase the sum by 5, we need to shift 5 students from b to c.
∴ Least possible value of c is 5.
⇒ The difference between the maximum and minimum possible number of students who like all the three drinks = 52 – 5 = 47
Hence, option (b).
Workspace:
Students in a college have to choose at least two subjects from chemistry, mathematics and physics. The number of students choosing all three subjects is 18, choosing mathematics as one of their subjects is 23 and choosing physics as one of their subjects is 25. The smallest possible number of students who could choose chemistry as one of their subjects is
- (a)
21
- (b)
20
- (c)
19
- (d)
22
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
The following Venn diagram can be drawn from the given information.

Since students must choose at least 2 subjects, there will be no one who chose a single subject.
Now, maximum number of students who choose only Math and Physics can be 5. (∵ 23 students chose Math)
Hence, for Physics we still have 25 – 18 – 5 = 2 students left.
These 2 students will have to chose Chemistry along with Physics.
∴ Least number of students who can choose Chemistry = 2 + 18 = 20.
Hence, option (b).
Workspace:
How many of the integers 1, 2, … , 120, are divisible by none of 2, 5 and 7?
- (a)
42
- (b)
41
- (c)
40
- (d)
43
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
There are total 120 numbers given.
Integers not divisible by 2, 5 and 7 = 120 – (numbers that are divisible by at least one of 2, 5 and 7)
We know, n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(C ∩ A) + n(A ∩ B ∩ C).
n(x) = number of multiples of x.
∴ n(2 ∪ 5 ∪ 7) = n(2) + n(5) + n(7) - n(2 ∩ 5) - n(5 ∩ 7) - n(7 ∩ 2) + n(2 ∩ 5 ∩ 7)
⇒ n(2 ∪ 5 ∪ 7) = n(2) + n(5) + n(7) - n(10) - n(35) - n(14) + n(70)
⇒ n(2 ∪ 5 ∪ 7) = 60 + 24 + 17 - 12 - 3 - 8 + 1 = 79.
Now, Integers not divisible by 2, 5 and 7 = 120 – (numbers that are divisible by at least one of 2, 5 and 7)
= 120 – 79 = 41
∴ Out of 120 numbers given, 41 numbers are not divisible by any of 2, 5 and 7.
Hence, option (b).
Workspace:
A club has 256 members of whom 144 can play football, 123 can play tennis, and 132 can play cricket. Moreover, 58 members can play both football and tennis, 25 can play both cricket and tennis, while 63 can play both football and cricket. If every member can play at least one game, then the number of members who can play only tennis is
- (a)
45
- (b)
43
- (c)
32
- (d)
38
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
From observing the data given, we find that it is a closed 3 set Venn diagram.
Let the three sports be F, T and C for Football, Tennis and Cricket respectively
n(FUTUC) = 256,
n(F) = 144, n(T) = 123, n(C) = 132,
n(F∩T) = 58, n(C∩T) = 25, n(F∩C) = 63
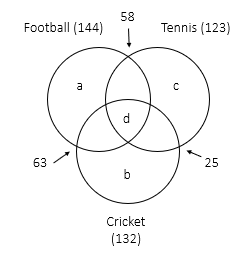
We know that (AUBUC) = n(A) + n(B) +n(C) - n(A∩B) - n(B∩C) - n(C∩A) + n(A∩B∩C)
So, 256 = 144 + 123 + 132 - 58 - 25 - 63 + n(F∩T∩C)
n(F∩T∩C) = 256 - 144 + 123 +132 - 146
n (F∩T∩C) = 256 - 253 = 3
Now, n(Students who play only Tennis) = 123 - (55 + 3 + 22) = 123 - 80
n(Students who play only Tennis) = 43 students.
Hence, option (b).
Workspace:
Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is
Answer: 52
Join our Telegram Group for CAT Preparation.
Text Explanation :
Every student who studies P also studies. It means there is not one who studies only P.
Let ‘a’ and ‘c’ denote the number of students studying only H and only E respectively while ‘b’ denote the number of students studying H and P (but not E) and ‘d’ denote the number of students studying E and P (but not H).
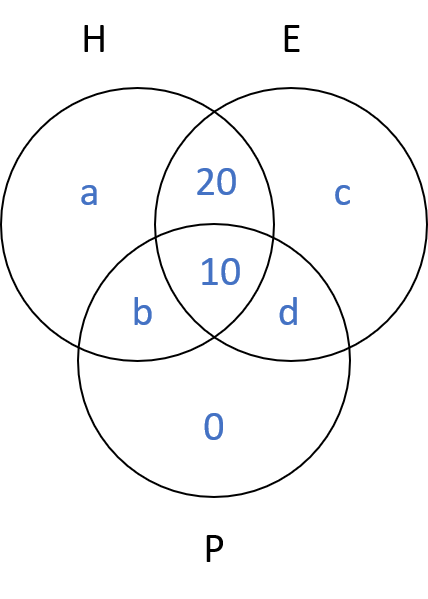
Total number of students = a + b + c + d + 30 = 74
⇒ a + b + c + d = 44 ...(1)
Number of students studying H = Number of students studying E
∴ a + b = c + d ...(2)
From (1) and (2) we get,
a + b = c + d = 22
∴ The number of students studying in H = 22 + 30 = 52
Hence, 52.
Workspace:
If among 200 students, 105 like pizza and 134 like burger, then the number of students who like only burger can possibly be
- (a)
26
- (b)
96
- (c)
93
- (d)
23
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
The minimum number of students who like only burger = 134 – 105 = 29
We can eliminate options (a) and (d).
The maximum number of students who like only burger = 200 – 105 = 95
We can eliminate option (b).
Thus, it can be concluded that the number of students who like only burger can possibly be 93.
Hence, option (c).
Workspace:
A survey was conducted of 100 people to find out whether they had read recent issues of Golmal, a monthly magazine. The summarized information regarding readership in 3 months is given below:
Only September: 18; September but not August: 23; September and July: 8; September: 28; July: 48; July and August: 10; None of the three months: 24.
What is the number of surveyed people who have read exactly two consecutive issues (out of the three)?
- (a)
7
- (b)
9
- (c)
12
- (d)
14
- (e)
17
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

100 – 24 = 76 had read at least one issue.
If x people read all the three issues, then (8 – x) people read only the September and July issues.
23 people read the September issue but not the August issue.
∴ 18 + 8 – x = 23
∴ x = 3
As 28 people read the September issue, [28 – (8 – 3) – 3 – 18] = 2 people read only the August and September issues.
As 10 people read the July and August issues, 10 – 3 = 7 people read only the July and August issues.
∴ The number of people who have read exactly two consecutive issues = 7 + 2 = 9
[Note: July and September are not consecutive months, hence we will not consider them.]
Hence, option (b).
Workspace:
Answer the following question based on the information given below.
New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Buddhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.
What is the number of projects in which Gyani alone is involved?
- (a)
Uniquely equal to zero
- (b)
Uniquely equal to 1
- (c)
Uniquely equal to 4
- (d)
Cannot be determined uniquely
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :

Let a be the number of projects in which only Gyani is involved, g be the number of projects in which only Buddhi is involved and c be the number of projects in which only Medha is involved.
From the data, d = 6
b + d = 14
∴ b = 8
Also, e = 3 and f = 2
It is given that
a + g = b + c + d + f
∴ a − c + g = 16 … (i)
Number of projects involving more than 1 consultant = 6 + 8 + 2 + 3 = 19
∴ Total number of projects = 2 × 19 − 1 = 37
a + b + c + d + e + f + g = 2 × (b + d + e + f) − 1
∴ a + c + g = 19 − 1 = 18 … (ii)
Solving (i) and (ii), we get,
c = 1 and a + g = 17
∴ a cannot be determined uniquely.
Hence, option (d).
Workspace:
What is the number of projects in which Medha alone is involved?
- (a)
Uniquely equal to zero
- (b)
Uniquely equal to 1
- (c)
Uniquely equal to 4
- (d)
Cannot be determined uniquely
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

Let a be the number of projects in which only Gyani is involved, g be the number of projects in which only Buddhi is involved and c be the number of projects in which only Medha is involved.
From the data, d = 6
b + d = 14
∴ b = 8
Also, e = 3 and f = 2
It is given that
a + g = b + c + d + f
∴ a − c + g = 16 … (i)
Number of projects involving more than 1 consultant = 6 + 8 + 2 + 3 = 19
∴ Total number of projects = 2 × 19 − 1 = 37
a + b + c + d + e + f + g = 2 × (b + d + e + f) − 1
∴ a + c + g = 19 − 1 = 18 … (ii)
Solving (i) and (ii), we get,
c = 1 and a + g = 17
we get, c = 1
∴ Number of projects in which Medha alone is involved = 1
Hence, option (b).
Workspace:
A survey on a sample of 25 new cars being sold at a local auto dealer was conducted to see which of the three popular options- air conditioning, radio and power windows- were already installed. The survey found
- 15 had air conditioning,
- 2 had air conditioning and power windows but no radios,
- 12 had radio,
- 6 had air conditioning and radio, but no power windows,
- 11 had power windows,
- 4 had radio and power windows and
- 3 had all three options.
What is the number of cars that had none of the options?
- (a)
4
- (b)
3
- (c)
1
- (d)
2
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, AC – Air Conditioning, R – Radio and PW – Power Windows
From the given conditions, we have the above Venn diagram.
When we add up all the values in the Venn diagram, we get 23 (15 + 5 + 1 + 2) cars.
∴ 2 (i.e. 25 − 23) cars don’t have any of the three options.
Hence, option (d).
Workspace:
Each question is followed by two statements A and B. Answer each question using the following instructions:
Answer (1) if the question can be solved by any one of the statements, but not the other one.
Answer (2) if the question can be solved by using either of the two statements.
Answer (3) if the question can be solved by using both the statements together and not by any one of them.
Answer (4) if the question cannot be solved with the help of the given data and more data is required.
Members in a club either speak French or Russian or both. Find the number of members in a club who speak only French.
A. There are 300 members in the club and the number of members who speak both French and Russian is 196.
B. The number of members who speak only Russian is 58.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let F represent the set of members speaking French and R represent the set of members speaking Russian.
Also, let x represent the number of members speaking only French.
Consider statement A:

Here, total number of members = 300
∴ Number of members who speak only Russian = 300 – 196 – x = 104 – x
However, we cannot find the value of x.
∴ Statement A alone is not sufficient.
Consider statement B:
We are given that the number of members speaking Russian = 58
∴ Statement B alone is not sufficient.
Consider both statements together:

We have, 104 – x = 58
∴ Number of members speaking only French, x = 104 – 58 = 46
∴ The question can be answered using both statements together.
Hence, option (c).
Workspace:
Choose 1; if the question can be answered by using one of the statements alone, but cannot be answered using the other statement alone.
Choose 2; if the question can be answered by using either statement alone.
Choose 3; if the question can be answered by using both statements together, but cannot be answered using either statement alone.
Choose 4; if the question cannot be answered even by using both statements together.
How many people are watching TV programme P?
- Number of people watching TV programme Q is 1000 and number of people watching both the programmes, P and Q, is 100.
- Number of people watching either P or Q or both is 1500.
- (a)
1
- (b)
2
- (c)
3
- (d)
4
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
From Statement A
Q = 1000
P ∩ Q = 100
This doesn’t gives any information regarding how many people are watching TV programme P
From Statement B
P ∪ Q = 1500
This statement alone is not sufficient.
Let’s combine the information in both the statements.
∴ P ∪ Q = P + Q − P ∩ Q
∴ 1500 = P + 1000 – 100
∴ P = 600
Hence, option (c).
Alternatively
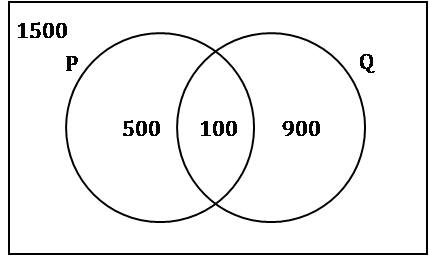
By combining both the statements together we can arrive at the above Venn diagram which gives the number of people watching programme P.
Hence, option (c).
Workspace:
In a survey of political preferences, 78% of those asked were in favour of at least one of the proposals: I, II and III.
50% of those asked favoured proposal I, 30% favoured proposal II and 20% favoured proposal III. If 5% of those asked favoured all three of the proposals, what percentage of those asked favoured more than one of the three proposals?
- (a)
10
- (b)
12
- (c)
17
- (d)
22
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let ‘a’ be the percentage of people who favoured exactly one proposal, ‘b’ be the percentage of people who favoured exactly by two proposals and ‘c’ be the percentage of people who favoured exactly three proposals.
a + b + c = 78......(i)
a + 2b + 3c = 100.....(ii)
(ii) – (i) implies b + 2c = 22
Since c = 5, b = 12
Required percentage = b + c = 12 + 5 = 17%.
Hence, option (c).
Workspace:
Direction: Answer the questions based on the following information.
A survey of 200 people in a community who watched at least one of the three channels — BBC, CNN and DD — showed that 80% of the people watched DD, 22% watched BBC and 15% watched CNN.
What is the maximum percentage of people who can watch all the three channels?
- (a)
12.5%
- (b)
8.5%
- (c)
15%
- (d)
Data insufficient
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, a + b + c + d + e + f + g = 200 ...(i)
80% of the people watch DD implies
c + d + f + g = 160 ...(ii)
22% of the people watch BBC implies
a + d + e + g = 44 ...(iii)
15% of the people watch CNN implies
b + e + f + g = 30 ...(iv)
(ii) + (iii) + (iv) gives
a + b + c + 2(d + e + f) + 3g = 234
Subtracting (i) from this equation,
d + e + f + 2g = 34 ...(v)
To maximize g, in equation (v), we put d = e = f = 0
∴ Maximum value of g = = 17
∴ Required percentage = × 100 = 8.5%
Hence, option (b).
Workspace:
If 5% of people watched DD and CNN, 10% watched DD and BBC, then what percentage of people watched BBC and CNN only?
- (a)
2%
- (b)
5%
- (c)
8.5%
- (d)
Cannot be determined
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, a + b + c + d + e + f + g = 200 ...(i)
80% of the people watch DD implies
c + d + f + g = 160 ...(ii)
22% of the people watch BBC implies
a + d + e + g = 44 ...(iii)
15% of the people watch CNN implies
b + e + f + g = 30 ...(iv)
(ii) + (iii) + (iv) gives
a + b + c + 2(d + e + f) + 3g = 234
Subtracting (i) from this equation,
d + e + f + 2g = 34 ...(v)
5% of people watch DD and CNN implies
f + g = 10 ...(vi)
10% of people watch DD and BBC implies
d + g = 20 ...(vii)
(v) – (vi) – (vii) gives
e = 4
∴ Required percentage = × 100 = 2%
Workspace:
Referring to the previous question, what percentage of people watched all the three channels?
- (a)
3.5%
- (b)
0%
- (c)
8.5%
- (d)
Cannot be determined
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, a + b + c + d + e + f + g = 200 ...(i)
80% of the people watch DD implies
c + d + f + g = 160 ...(ii)
22% of the people watch BBC implies
a + d + e + g = 44 ...(iii)
15% of the people watch CNN implies
b + e + f + g = 30 ...(iv)
(ii) + (iii) + (iv) gives
a + b + c + 2(d + e + f) + 3g = 234
Subtracting (i) from this equation,
d + e + f + 2g = 34 ...(v)
From equation (v), we have
(d + 4 + f) + 2g = 34
⇒ (d + f) + 2g = 30
Since we cannot find the values of d and f, the value of g cannot be ascertained.
Workspace:
In a locality, two-thirds of the people have cable TV, one-fifth have VCR, and one-tenth have both. What is the fraction of people having either cable-TV or VCR?
- (a)
- (b)
- (c)
- (d)
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Probability of people having cable-TV = 2/3
Probability of people having VCR = 1/5
Probability of people having both = 1/10
∴ Probability of people having cable TV or VCR = = =
Hence, option (d).
Workspace:
Answer the next 3 questions based on the information given below:
Ghoshbabu is staying at Ghosh Housing Society, Aghosh Colony, Dighospur, Calcutta. In Ghosh Housing Society 6 persons read daily Ganashakti and 4 read Anand Bazar Patrika; in his colony there is no person who reads both. Total number of persons who read these two newspapers in Aghosh Colony and Dighospur is 52 and 200 respectively. Number of persons who read Ganashakti in Aghosh Colony and Dighospur is 33 and 121 respectively; while the persons who read Anand Bazar Patrika in Aghosh Colony and Dighospur are 32 and 117 respectively.
Number of persons in Dighospur who read only Ganashakti is
- (a)
121
- (b)
83
- (c)
79
- (d)
127
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
The data can be represented in the following Venn diagrams.



Number of persons in Dighoshpur who read only Ganashakti = 121 - 38 = 83.
Hence, option (b).
Workspace:
Number of persons in Aghosh Colony who read both of these newspapers is
- (a)
13
- (b)
20
- (c)
19
- (d)
14
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
The data can be represented in the following Venn diagrams.



Number of persons in Aghosh Colony who read both the newspapers = 13.
Workspace:
Number of persons in Aghosh Colony who read only one paper
- (a)
29
- (b)
19
- (c)
39
- (d)
20
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
The data can be represented in the following Venn diagrams.



Number of persons in Aghosh Colony who read only 1 newspaper = 20+19 = 39.
Workspace:
Out of 100 families in the neighbourhood, 45 own radios, 75 have TVs, 25 have VCRs. Only 10 families have all three and each VCR owner also has a TV. If 25 families have radio only, how many have only TV?
- (a)
30
- (b)
35
- (c)
40
- (d)
45
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :

Since each VCR owner also has a TV, therefore, 15 families own both TV and VCR but not Radio.
Since 25 families have radio only, therefore, 10 families own both TV and Radio but not VCR.
Hence, number of families having only TV = 75 – 10 – 10 – 15 = 40.
Hence, option (c).
Workspace:
Amar, Akbar, and Anthony came from the same public school in the Himalayas. Every boy in that school either fishes for trout or plays frisbee. All fishermen like snow while no frisbee player likes rain. Amar dislikes whatever Akbar likes and likes whatever Akbar dislikes. Akbar likes rain and snow. Anthony likes whatever the other two like. Who is a fisherman but not a frisbee player?
- (a)
Amar
- (b)
Akbar
- (c)
Anthony
- (d)
None
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Since Akbar likes rain, he cannot be a frisbee player (as no frisbee player likes rain). And since every boy in the school does one of the two, Akbar has to be a fisherman.
Hence, option (b).
Workspace:
Fifty college teachers are surveyed as to their possession of colour TV, VCR and tape recorder. Of them, 22 own colour TV, 15 own VCR and 14 own tape recorders. Nine of these college teachers own exactly two items out of colour TV, VCR and tape recorder; and, one college teacher owns all three. How many of the 50 teachers own none of the three, colour TV, VCR or tape recorder?
- (a)
4
- (b)
9
- (c)
10
- (d)
11
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let us find out how many teachers own at least one of the three items.
We konw, A∪B∪C = A + B + C – (exactly two of A, B and C) - 2(all three)
∴ TV∪VCR∪TR = 22 + 15 + 14 - (9) - 2(1) = 40
∴ 40 people own at least one of TV, VCR and Tape Recorder.
Hence the number of teachers owing none = 50 – 40 = 10.
Hence, option (c).
Workspace:
Answer the following questions based on the information given below:
There were a hundred schools in a town. Of these, the number of schools having a play – ground was 30, and these schools had neither a library nor a laboratory. The number of schools having a laboratory alone was twice the number of those having a library only. The number of schools having a laboratory as well as a library was one fourth the number of those having a laboratory alone. The number of schools having either a laboratory or a library or both was 35.
How many schools had none of the three viz., laboratory, library or play – ground?
- (a)
20
- (b)
5
- (c)
30
- (d)
35
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
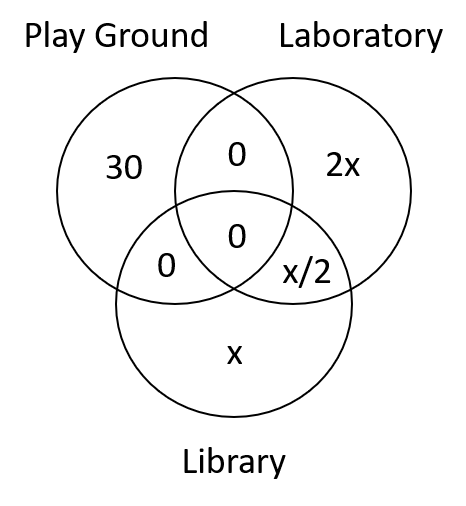
It is given that x + 2x + x/2 = 35.
Hence x = 10.
Total number of schools that had at least one of the three = 30 + 10 + 20 + 5 = 65.
Hence the number of schools having none of them = 100 – 65 = 35.
Hence, option (d).
Workspace:
What was the ratio of schools having laboratory to those having library?
- (a)
1 : 2
- (b)
5 : 3
- (c)
2 : 1
- (d)
2 : 3
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Number of schools having library = 15. And number of schools having laboratory = 25.
Hence the ratio = 25 : 15 = 5 : 3.
Hence, option (b).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report