Geometry - Circles - Previous Year CAT/MBA Questions
The best way to prepare for Geometry - Circles is by going through the previous year Geometry - Circles CAT questions. Here we bring you all previous year Geometry - Circles CAT questions along with detailed solutions.
Click here for previous year questions of other topics.
It would be best if you clear your concepts before you practice previous year Geometry - Circles CAT questions.
Join our Telegram Group for CAT Preparation.
All the vertices of a rectangle lie on a circle of radius R. If the perimeter of the rectangle is P, then the area of the rectangle is
- (a)
- 2PR
- (b)
- 2R2
- (c)
-
- (d)
- R2
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

Let the longer side of the rectangle be a and shorter side by b.
In the figure given, (2R)2 = a2 + b2
⇒ P = 2(a + b)
⇒ = a + b
Squaring both sides.
⇒ = a2 + b2 + 2ab
⇒ - 4R2 = 2ab
⇒ - 2R2 = ab
Area of the rectangle = a × b = ab =
Hence, option (b).
Workspace:
In a triangle ABC, AB = AC = 8 cm. A circle drawn with BC as diameter passes through A. Another circle drawn with center at A passes through B and C. Then, the area in sq. cm, of the overlapping region between the two circles is
- (a)
16(π - 1)
- (b)
32(π - 1)
- (c)
16π
- (d)
32π
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Since AB is the diameter of the smaller circle ⇒ ∠ACB = 90°.

In ∆ACB, AC2 + BC2 = AB2
⇒ AB = √(82 + 82) = 8√2
∴ Radius of smaller circle is ½ × 8√2 = 4√2
Diameter of larger circle = 8
Smaller Circle:
Area of green part = 1/2 × π × (4√2)2 = 16π
Larger Circle:
Area of blue part = Area of sector CAB – Area of ∆CAB
Area of blue part = 1/4 × π × 82 - 1/2 × 8 × 8 = 16π – 32
∴ Required area = 16π + (16π - 32) = 32(π - 1)
Hence, option (b).
Workspace:
A circle of diameter 8 inches is inscribed in a triangle ABC where ∠ABC = 90°. If BC = 10 inches then the area of triangle in square inches is.
Answer: 120
Join our Telegram Group for CAT Preparation.
Text Explanation :

Here, BM = BN = 4 (Radius of the circle)
BC = 10 cm, hence, MC = CO = 10 – 4 = 6 cm.
Let AN = x, hence, AO = x
In right ∆ABC,
AB2 + BC2 = AC2
⇒ (x + 4)2 + 102 = (x + 6)2
⇒ x2 + 16 + 8x + 100 = x2+ 12x + 36
⇒ 4x = 80
⇒ x = 20
∴ Area of triangle ABC = ½ × AB × BC = ½ × (20 + 4) × 10 = 120 sq. inches.
Hence, 120.
Workspace:
Let C1 and C2 be concentric circles such that the diameter of C1 is 2 cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm, of C1 is
Answer: 10
Join our Telegram Group for CAT Preparation.
Text Explanation :
The following figure can be drawn from the information given in the question.

Perpendicular OA will bisect the chord, hence AB = 3.
Let the radius of smaller circle be r, hence radius of bigger circle will be r + 1.
In right triangle OAB,
OB2 = OA2 + AB2
⇒ (r + 1)2 = r2 + 32
∴ r = 4
Diameter of C1 (the bigger circle) = 2(r + 1) = 10 cm.
Hence, 10.
Workspace:
Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to
- (a)
8.8
- (b)
6.6
- (c)
7.8
- (d)
7.2
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
The following figure can be drawn from the information given in the question.

In right triangle AOB, AB = 5 (Pythagorean triplet)
Also, OM is the altitude = = 2.4
In right triangle OMP,
OP2 = OM2 + MP2
⇒ 52 + (2.4)2 + MP2
⇒ MP =
⇒ PQ = 2MP = 2 × ≈ 2 × 4.4 = 8.8.
Hence, option (a).
Workspace:
The vertices of a triangle are (0, 0), (4, 0) and (3, 9). The area of the circle passing through these three points is
- (a)
123π/7
- (b)
205π/9
- (c)
14π/3
- (d)
12π/5
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
The diagram can be drawn as follows:

Height of the given triangle = 9 and base = 4
∴ Area of the triangle = = 18
We know area of a triangle = abc/4R
(where a, b, and c are the sides of the triangle and R is the circumradius)
a = AB = 4 units
b = BC = units
c = AC = units
The sides of the triangle are 4, √82 and √90
⇒ 18 =
⇒ R =
∴ Area of the circumcircle = πR2 =
Hence, option (b).
Workspace:
In a circle of radius 11 cm, CD is a diameter and AB is a chord of length 20.5 cm. If AB and CD intersect at a point E inside the circle and CE has length 7 cm, then the difference of the lengths of BE and AE, in cm, is
- (a)
0.5
- (b)
2.5
- (c)
3.5
- (d)
1.5
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
The circle can be drawn as shown below. Diameter of the circle = 2 × 11 = 22 cm.

CE = 7, so ED = CD − CE = 22 − 7 = 15.
Let AE be x units, so EB = AB − AE = 20.5 − x.
Using the intersecting chords theorem; AE × EB = CE × ED.
∴ x(20.5 − x) = 7 × 15
Solving this equation, we get x = 10.5, 10.
So, if (AE, BE) = (10.5, 10) or (10,10.5)
Required difference = |BE − AE| = |10.5− 10| = 0.5.
Hence, option (a).
Workspace:
AB is a diameter of a circle of radius 5 cm. Let P and Q be two points on the circle so that the length of PB is 6 cm, and the length of AP is twice that of AQ. Then the length, in cm, of QB is nearest to
- (a)
7.8
- (b)
8.5
- (c)
9.3
- (d)
9.1
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :
Since diameter subtends an angle of 90° at any point on the circumference, ∆APB is a right angled triangle.
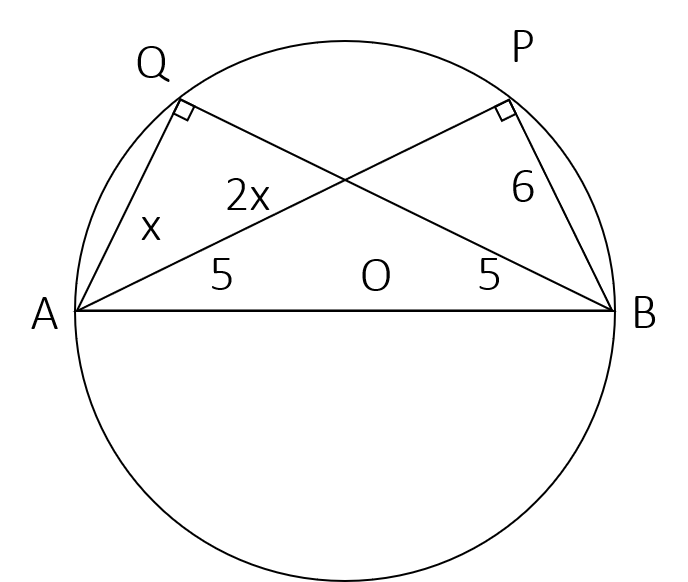
So AB2 = AP2 + PB2
⇒ 102 = (2x)2 + 62
∴ x = 4.
∆AQB is also a right angled triangle, so AB2 = AQ2 + QB2
∴ 102 = x2 + QB2
Put x = 4 to get QB = √84 = 9.165 ≈ 9.1 cm.
Hence, option (d).
Workspace:
Two circles, each of radius 4 cm, touch externally. Each of these two circles is touched externally by a third circle. If these three circles have a common tangent, then the radius of the third circle, in cm, is
- (a)
π/3
- (b)
1
- (c)
1/√2
- (d)
√2
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let the radius of the third circle be ‘x’ cm.
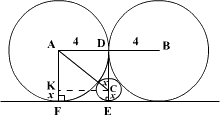
AF = DE = 4 cm ⇒ AK = DC = (4 – x) cm
In ∆ADC, AC2 = AD2 + DC2.
(4 + x)2 = 42 + (4 – x)2
∴ x = 1.
Hence, option (a).
Workspace:
Let ABC be a right-angled triangle with hypotenuse BC of length 20 cm. If AP is perpendicular on BC, then the maximum possible length of AP, in cm, is
- (a)
10
- (b)
8√2
- (c)
6√2
- (d)
5
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
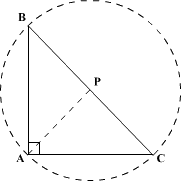
∠BAC = 90°, so BC can be considered diameter of a circle with center anywhere on BC.
AP is maximum when it is the perpendicular bisector from the vertex to the hypotenuse. So, BP = PC = 20/2 = 10. This implies that P is the center of the circle.
∴ AP = BP = PC = 10 cm.
Hence, option (b).
Workspace:
In a circle, two parallel chords on the same side of a diameter have lengths 4 cm and 6 cm. If the distance between these chords is 1 cm, then the radius of the circle, in cm, is
- (a)
√12
- (b)
√13
- (c)
√11
- (d)
√14
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

OP⊥ PQ and OQ⊥ AB
In a circle perpendicular to the chord bisects the chord.
∴ CP = PD = 3 and AQ = QB = 2
Let OP = x cm
OC = OB
In ∆OPC and ∆OQB
∴ Radius = =
∴ =
∴ x = 2
∴ Radius = = √13
Hence, option (b).
Workspace:
In a circle with center O and radius 1 cm, an arc AB makes an angle 60 degrees at O. Let R be the region bounded by the radii OA, OB and the arc AB. If C and D are two points on OA and OB, respectively, such that OC = OD and the area of triangle OCD is half that of R, then the length of OC, in cm, is
- (a)
(π/6)1/2
- (b)
(π/3√3)1/2
- (c)
(π/4√3)1/2
- (d)
(π/4)1/2
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Let OC = OD = x

△OCD is an equilateral triangle of side x. [All angles are 60 degree.]
A(△OCD) =
A(sector O-AB) = =
By the given condition,
=
∴ x2 =
∴ x =
Hence, option (b).
Workspace:
A chord of length 5 cm subtends an angle of 60° at the centre of a circle. The length, in cm, of a chord that subtends an angle of 120° at the centre of the same circle is
- (a)
- (b)
- (c)
2π
- (d)
8
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :
The triangle formed by joining the endpoints of the chord of a circle with the center of the circle is an isosceles triangle because the two sides of the triangle (radii of the circle) are congruent. If the angle subtended by the chord at the center of the circle is 60 degrees, the triangle is an equilateral triangle. Therefore the side of the triangle and the radius of the circle is equal to the side of the triangle = 5 cm.
Now we have the following

OP is perpendicular to the chord AB. Therefore P is the midpoint of chord AB. Further, OA and OP are the radii of the circle. Therefore triangles OAP and OBP are congruent. Therefore triangle OAP and OBP are 30-60-90 triangles.
We have,
Therefore,
Therefore,
Hence, option (a).
Workspace:
On a triangle ABC, a circle with diameter BC is drawn, intersecting AB and AC at points P and Q, respectively. If the lengths of AB, AC, and CP are 30 cm, 25 cm, and 20 cm respectively, then the length of BQ, in cm, is
Answer: 24
Join our Telegram Group for CAT Preparation.
Text Explanation :

Since points P and Q lie on the circumference of the circle drawn with BC as diameter, angles BPC and BQC are right angled triangles.
Now, area of triangle ABC = =
Therefore, BQ = = = 24
Hence, 24.
Workspace:
Let ABC be a right-angled isosceles triangle with hypotenuse BC. Let BQC be a semi-circle, away from A, with diameter BC. Let BPC be an arc of a circle centered at A and lying between BC and BQC. If AB has length 6 cm then the area, in sq. cm, of the region enclosed by BPC and BQC is:
- (a)
9π - 18
- (b)
18
- (c)
9π
- (d)
9
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
AB = a (a = 6)
BC = a√2
BCQB is a semicircle of radius = half of BC =
Area of semicircle BCQB = ½ × π × = ¼ × π × a2
ACPBA is a quarter circle (quadrant) of radius a.
Area of BCPB = Area of sector ABPCA - Area of triangle ABC
= ¼ × π × a2 - Area of triangle ABC
Now, Area of CPBQC = Area of semicircle CQB - Area of CPBC
= ¼ × π × a2 - ( ¼ × π × a2 - Area of triangle ABC)
= Area of triangle ABC
∴ Area of region enclosed by CPBQC = Area of ∆ABC = ½ × 6 × 6 = 18.
Hence, option (b).
Workspace:
Two circles, both of radii 1 cm, intersect such that the circumference of each one passes through the centre of the circle of the other. What is the area (in sq cm) of the intersecting region?
- (a)
- (b)
- (c)
- (d)
- (e)
Answer: Option E
Join our Telegram Group for CAT Preparation.
Text Explanation :

Let O and P be the centres of the circles.
OR = OP = PR = 1cm
∴ ∆PRO is an equilateral triangle.
∴ m ∠ROP = 60°
∴ m ∠ROS = 120°
Now, area of the intersecting region = 2(area of sector O-RPS – area of ∆ORS)
= 2(area of sector O-RPS – area of ∆PRO) [area of ∆PRO = area of ∆ORS]
Area of sector O - RPS = =
Area of ∆PRO =
∴ Area of the intersecting region = - =
Hence, option (e).
Workspace:
Two circles with centres P and Q cut each other at two distinct points A and B. The circles have the same radii and neither P nor Q falls within the intersection of the circles. What is the smallest range that includes all possible values of the angle AQP in degrees?
- (a)
Between 0 and 90
- (b)
Between 0 and 30
- (c)
Between 0 and 60
- (d)
Between 0 and 75
- (e)
Between 0 and 45
Answer: Option C
Join our Telegram Group for CAT Preparation.
Text Explanation :

P and Q do not lie within the intersection of the two circles.
So they lie on the circumferences or outside the circumferences.
Case 1: If they lie on the circumferences, then ΔAPQ forms an equilateral triangle.
So, m ∠AQP = 60°
Case 2: From the diagram, if they lie outside the circumferences,
m ∠AQ'P' < 60°
Also, m ∠AQP would be 0° if A, Q and P were collinear.
But as P and Q cut each other in two distinct points, A, Q and P cannot be collinear.
∴ m ∠AQP > 0°
∴ The value, m ∠AQP lies between 0° and 60°
Hence, option (c).
Workspace:
A semicircle is drawn with AB as its diameter. From C, a point on AB, a line perpendicular to AB is drawn meeting the circumference of the semicircle at D. Given that AC = 2 cm and CD = 6 cm, the area of the semicircle (in sq. cm.) will be:
- (a)
32π
- (b)
50π
- (c)
40.5π
- (d)
81π
- (e)
undeterminable
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

Let CB = x cm
In a right triangle if DC is the altitude from right vertex, DC2 = AC × BC
∴ 62 = 2 × x
⇒ x = 18
⇒ AB = 2 + 18 = 20
∴ Diameter of the semicircle = 20
⇒ Radius of the semicircle = 10
∴ Area = 1/2 × π × 102 = 50π sq. cm.
Hence, option (b).
Workspace:
Two identical circles intersect so that their centres, and the points at which they intersect, form a square of side 1 cm. The area in sq. cm of the portion that is common to the two circles is
- (a)
- (b)
- (c)
- (d)
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
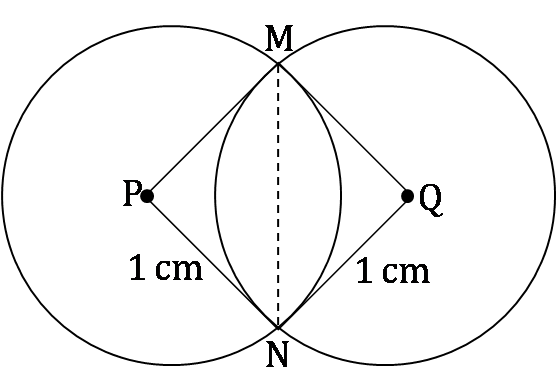
Let the two circles with centres P and Q intersect at M and N.
Quadrilateral PMQN is a square.
m ∠MPN = m ∠MQN = 90°
The area common to both the circles = 2(Area of sector P-MN – Area of ∆PMN)
Hence, option (b).
Workspace:
What is the distance in cm between two parallel chords of lengths 32 cm and 24 cm in a circle of radius 20 cm?
- (a)
1 or 7
- (b)
2 or 14
- (c)
3 or 21
- (d)
4 or 28
Answer: Option D
Join our Telegram Group for CAT Preparation.
Text Explanation :


The two chords AB and CD can be on the same side or the opposite sides of the centre O.
Let M and N be the midpoints of AB and CD.
∴ MN is the distance between the two chords.
MB = 12 cm and ND = 16 cm
OM and ON are perpendicular to AB and CD respectively.
ON2 = OD2 - ND2 (By Pythagoras theorem)
⇒ ON2 = 202 – 162
⇒ ON = 12 cm
Similarly,OM2 = OB2 - MB2
⇒ OM = 16 cm
Case 1: AB and BC are on the same side of the centre.
MN = OM – ON = 4 cm
Case 2: AB and BC are on opposite sides of the centre.
MN = OM + ON = 28 cm
Hence, option (d).
Workspace:
Four points A, B, C and D lie on a straight line in the X-Y plane, such that AB = BC = CD, and the length of AB is 1 metre. An ant at A wants to reach a sugar particle at D. But there are insect repellents kept at points B and C. The ant would not go within one metre of any insect repellent. The minimum distance in metres the ant must traverse to reach the sugar particle is
- (a)
- (b)
1 + π
- (c)
- (d)
5
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

The ant will not go into the circles with centers B and C and radius = 1 m
The minimum distance that the ant has to traverse = the distance of the path A-H-G-D
HG = 1 m
AH = GD = × Circumference of circle =
AH + GD = π m
∴ The ant must traverse (1 + π)m.
Hence, option (b).
Workspace:
In the following figure, the diameter of the circle is 3 cm. AB and MN are two diameters such that MN is perpendicular to AB. In addition, CG is perpendicular to AB such that AE : EB = 1 : 2, and DF is perpendicular to MN such that NL : LM = 1 : 2. The length of DH in cm is

- (a)
- (b)
- (c)
- (d)
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
AO = OD = 1.5 cm
AE + EB = 3 cm and AE : EB = 1 : 2
∴ AE = 1 cm and EB = 2 cm
OE = AO – AE = 1.5 – 1 = 0.5 cm
Similarly, NL = 1 cm, LM = 2 cm, and OL = 0.5 cm
OEHL is a square as all its angles are right angles and OE = OL
∴ EH = HL = 0.5 cm
In ∆ODL, OD2 = OL2 + DL2
1.5² = 0.5² + (0.5 + DH)²
2.25 = 0.25 + 0.25 + DH + DH²
DH² + DH – 1.75 = 0
DH = = (DH > 0)
Hence, option (b).
Workspace:
P, Q, S, and R are points on the circumference of a circle of radius r, such that PQR is an equilateral triangle and PS is a diameter of the circle. What is the perimeter of the quadrilateral PQSR?
- (a)
2r(1 + )
- (b)
2r(2 + )
- (c)
r(1 + )
- (d)
2r +
Answer: Option A
Join our Telegram Group for CAT Preparation.
Text Explanation :

∆ PQR is an equilateral triangle and PS is the diameter.
∴ m ∠PQS = m ∠PRS = 90° (angles subtended in a semi-circle)
and m ∠PQM = m ∠PRM = m ∠QPR = 60° (each angle in an equilateral triangle = 60°)
PS bisects ∠QPS as it is the median of ∆PQR.
m ∠PMQ = m ∠PMR = 90°
∴ m ∠QPS = m ∠RPS = 30°
∴ m ∠PSQ = m ∠PSR = 60°
Radius = r
∴ PS = 2r
As ∆ PQS, ∆ PQM, ∆ MQS are 30°-60°-90° triangles,
QS = r, PQ = √3r
Similarly, RS = r and PR = √3r
∴ Perimeter of quadrilateral PQRS = 2r + 2√3r = 2r(1 + √3)
Hence, option (a).
Workspace:
Answer the following question based on the information given below.
In the adjoining figure, I and II are circles with centres P and Q respectively. The two circles touch each other and have a common tangent that touches them at points R and S respectively. This common tangent meets the line joining P and Q at O. The diameters of I and II are in the ratio 4 : 3. It is also known that the length of PO is 28 cm.

What is the ratio of the length of PQ to that of QO?
- (a)
1 : 4
- (b)
1 : 3
- (c)
3 : 8
- (d)
3 : 4
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :

ΔSQO ~ ΔRPO
⇒ = =
⇒ =
⇒ 42 = 56 – 7x
⇒ x = 2
⇒ PQ = 7 cm, OQ = 21 cm
∴ PQ : OQ = 1 : 3
Hence, option (b).
Workspace:
What is the radius of the circle II?
- (a)
2 cm
- (b)
3 cm
- (c)
4 cm
- (d)
5 cm
Answer: Option B
Join our Telegram Group for CAT Preparation.
Text Explanation :
Radius of circle II = 1.5 × 2 = 3 cm.
Hence, option (b).
Alternately,
We can solve this question and the previous question together using options as follows:
Consider each of the options in this question.
Option (a): If the radius of circle II is 2, the radius of I is 8/3. PQ is then 14/3 and OQ is 70/3.
∴ PQ : OQ = 1 : 5, which is not there in the options of the previous question.
Option (b): If the radius of circle II is 3, the radius of I is 4. PQ is then 7 and OQ is 21.
∴ PQ : OQ = 1 : 3, which is there in the options of the previous question. This is possible.
Option (c): If the radius of circle II is 4, the radius of I is 16/3. PQ is then 28/3 and OQ is 56/3.
∴ PQ : OQ = 1 : 2, which is not there in the options of the previous question.
Option (d): If the radius of circle II is 5, the radius of I is 20/3. PQ is then 35/3 and OQ is 49/3.
∴ PQ : OQ = 5 : 7, which is not there in the options of the previous question.
∴ The radius of circle II is 3 and PQ : OQ = 1 : 3
Hence, option (b).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report