CAT 2018 QA Slot 2 | Previous Year Questions

Answer: 50

Explanation :

If both cars travel towards east, they meet in 7 hours. Therefore the faster car starting from A covers the distance of separation of 350 km in 7 hours. Therefore,

$a-b=\frac{350}{7}=50$

Hence, 50.

Answer: 5

Explanation :

The speeds of both the cars in the three legs of the journey are equal. Therefore the second car will reach point B as many minutes after the first car as it started after the first car.

For the first 50 km of the journey, the speed of the cars is 100 kmph. Therefore, the first car reaches a distance of 20 km

from point A after = $\frac{20}{100}=0.2$ hours

= 0.2 × 60 = 12 minutes.

When the first car reaches point B, the second car is 12 minutes away from point B. The speed of the car in the last 50 km distance is 25 kmph. Therefore the distance of the second car from point

$B=25\times \frac{12}{60}=5 km$

Hence, 5.

Answer: 105

Explanation :

As the AM of x, y and z is 80,
⇒ x + y + z = 80 × 3 = 240   … (1)

As the AM of x, y, z, u and v is 75
⇒ x + y + z + u + v = 75 × 5 = 375   … (2)

Subtracting equation (1) from (2), we get
u + v = 135

$\therefore \frac{x+y}{2}+\frac{y+z}{2}=135$

∴ x + 2y + z = 270 … (3)

Solving equations (1) and (3), we get
⇒ y = 30

∴ x + z = 210.

Now, since x  ≥  z, the minimum value of x = 105.

Hence, 105.

Answer: 48

Explanation :

Suppose the inlet pipes of type A fill in water at the rate ‘a’ units per minute and the inlet pipes of type B fill in water at the rate ‘b’ units per minute.

Therefore we have the following

30(10a + 45b) = 60(8a + 18b)
∴ 300a + 1350b = 480a + 1080b
∴ 180a = 270b
∴ a = 1.5b

Total capacity of the tank
= 300a + 1350b = 300(1.5b) + 1350b
= 1800b

If 7 inlet pipes of type A and 27 inlet pipes of type B are opened, the volume of water filled in every minute

= 7a + 27b = 7(1.5b) + 27b = 37.5b

Therefore the number of minutes taken to fill the tank

$=\frac{\mathrm{1800b}}{37.\mathrm{5b}}=\mathrm{48\; minutes}$

Hence, 48.

Answer: 4000

Explanation :

The only difference in the two situations is that in the second situation, Gopal lent Rs. Y more to Ishan than in the first situation. Therefore the additional interest retained by Gopal = 0.1Y.

Therefore 0.1.Y = 150 or Y = 1500.

Now, Ankit lent Gopal Rs. X at 8% interest. Therefore the interest retained by Ankit = Rs. 0.08X.

Gopal lent Ishan Rs. (X + 1500) at 10% interest.

Therefore the interest retained by Gopal = 0.1X + 150 - 0.08X = 0.02X + 150

Therefore, 0.08X = 0.02X + 1500 or X = 2500.

Therefore the value of X + Y = 4000.

Hence, 4000.

Answer: Option C

Explanation :

Suppose ‘R’ and ‘G’ are the number of units of work completed by Ramesh and Ganesh everyday. Therefore the total work to be completed = 16(R + G) = 16R + 16G

For the first 7 days, both work at 100% efficiency and for the remaining 10 days, Ramesh works at 70% efficiency. Therefore the total work to be completed = 7(R + G) + 10(0.7R + G) = 14R + 17G

∴ 16R + 16G = 14R + 17G or G = 2R

Now if only Ganesh had worked after Ramesh fell sick:
Work to be done = 9(G + R) = 9(2R + R) = 27R
Efficiency of Ganesh = G = 2R

∴ Time taken to finish the remaining work = 27R/2R = 13.5 days.

Hence, option (c).

Answer: Option C

Explanation :

We have the following:
 

 

The cars 3 and 1 meet at point Q. Therefore, the car 3 covers 100 km in the time the car 1 covers 200 km. Therefore the ratio of the speeds of cars 3 and 1 i.e., C₃ : C₁ = 1 : 2.

The cars 2 and 3 meet at point P. Therefore, the car 2 covers 100 km in the time the car 3 covers 200 km. Therefore the ratio of the speeds of cars 3 and car 2 i.e., C₃ : C₂ = 2 : 1.

Combining the two statements, the ratio of the speeds of three cars i.e., C₃: C₂ : C₁ = 4 : 2 : 1.

Hence, option (c).

Answer: Option C

Explanation :

Originally, the volume of alcohol = 4 times the volume of water. Therefore, original percentage of alcohol = 80% and original volume of water = 20%.

When 10% of the mixture is removed and replaced with water, the percentage of alcohol remained in the mixture

= $80\%\times {\left(\frac{9}{10}\right)}^2$ = 64.8%

Therefore the percentage of water in the mixture = (100 - 64.8)% = 35.2%.

Hence, option (c).

Answer: Option D

Explanation :

The time taken by pump A alone to fill the tank completely = t hours.

The time taken by pump B alone to fill the tank completely = ‘t - 2’ hours.

On Wednesday, pump A was used for 3 hour less and pump B was used for 2 hours to complete the remaining work.
⇒ Work done by A in 3 hours = Work done by B in 2 hours.
⇒ efficiency of A : efficiency of B = 2 : 3

Let efficiency of A be '2x' and that of B be '3x'.

Now, total work is done by B in (t - 2) hours and by A in t hours.
⇒ 3x × (t - 2) = 2x × t
⇒ 3(t - 2) = 2t
⇒ t = 6 hours

∴ The tank starts filling at 2 pm.

If both pumps start filling, their combined efficiency = 5x
Total work to be done = 3x(t - 2) = 12x

⇒ Time taken to fill the tank = 12x/5x = 2.4 hours = 2 hours 24 minutes.

Therefore on Thursday, the tank will be completely full at 4.24 pm.

Hence, option (d).

Answer: Option A

Explanation :

Suppose the concentrations of the solutions A, B and C are ‘a’, ‘b’ and ‘c’ respectively.

If the three solutions are mixed in the ratio 1 : 2 : 3, the resultant solution has 20% concentration. Therefore, we have

$\frac{a+2b+3c}{1+2+3}=20$ or a + 2b + 3c = 120   ...(1)

If the three solutions are mixed in the ratio 3 : 2 : 1, the resultant solution has 30% concentration. Therefore, we have

$\frac{3a+2b+c}{3+2+1}=30$ or 3a + 2b + c = 180   ...(2)

Multiplying equation (1) with 3 and (2) with 2 and equating both, we get

3a + 6b + 9c = 6a + 4b + 2c

⇒ 2b + 7c = 3a

Now, concentration of solution D = $\frac{2b+7c}{9}$ = $\frac{3a}{9}$ = $\frac{a}{3}$

Therefore the ratio of D's concentration to A's concentration $=\frac{a/3}{a}=\frac{1}{3}$

Hence, option (a).

Answer: Option B

Explanation :

Given numbers are a₁, a₂, a₃,..., a₅₁,100.

If the arithmetic mean of these 52 numbers is ‘x’, we have
a₁ + a₂ + a₃ + ... + a₅₁ + 100 = 52x   ...(1)

Given: the arithmetic mean of a₂, a₃, a₄,...,a₅₁, 100 is ‘x + 1’
a₂ + a₃ + ⋯ + a₅₁ + 100 = 51(x + 1) = 51x + 51   ...(2)

Solving (1) and (2), we get:
∴ a₁ = x − 51   ...(3)

Now for a₁ to be maximum possible, x has to be maximum possible.

For x to be maximum possible each of a₂, a₃, ..., till a₅₁ has to be maximum possible. But they are also distinct integers.
∴ Maximum value of
a₅₁ = 99 [it has to be an integer less than a₅₂]
a₅₀ = 98 [it has to be an integer less than a₅₁]
​​​​​​​...
a₂ = 50

⇒ a₂, a₃, ..., a₅₂ are consecutinve integers from 50 till 100.

⇒ Average of (a₂, a₃, ..., a₅₂) = 1/2 × (50 + 100) = 75 = x + 1 [From (2)]
⇒ x = 74

From (3)
⇒ a₁ = 74 - 51 = 23

Hence, option (b).

Answer: Option A

Explanation :

Suppose the original scores of Amal and Bimal are 11x and 14x respectively.

Suppose ‘y’ is the increase in their marks.

Therefore the new marks of Amal and Bimal are ‘11x + y’ and ‘14x + y’ respectively.

Therefore, we have $\frac{11x+y}{14x+y}=\frac{47}{56}$

∴ 616x + 56y = 658x + 47y

Solving for x and y, we get 14x = 3y

Therefore Bimal’s old marks = 14x = 3y and his new marks = 14x + y = 4y. Therefore the required ratio = 4:3.

Hence, option (a).

Answer: Option D

Explanation :

Suppose the mixture from drum 1 = 300x litres and the mixture from drum 2 = 400x litres. Therefore, we have the following

​​​​​​​

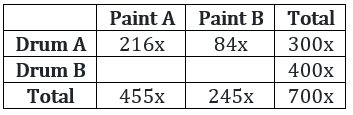
Therefore the volume of Paint A in Drum B = 455x – 216x = 239x and the volume of Paint B in Drum B = 245x − 84x = 161x.

Therefore the required ratio is 239 : 161.

Hence, option (d).

Answer: Option B

Explanation :

A 20% solution is mixed with x% solution in the ratio 1 : 3

Let 10 liters of 20% solution is mixed with 30 liters of x% solution.

Now, the total volume of the mixture = 40 liters.

This solution is mixed with 20% solution having equal volume.

∴ A total of 50 liters of 20% solutio is mixed with 30 liters of x% solution.

⇒ Final concentration = 31.25% = $\frac{20\%\times 50+x\times 30}{80}$

⇒ 2500 = 1000 + 30x
⇒ x = 50%

Hence, option (b).

Answer: Option B

Explanation :

The area of the triangle is 32 sq units.

Therefore, 32 = ½ × BC × height

Given, BC = 8

⇒ Height =  $\frac{2\times 32}{8}$ = 8 cm

Therefore Height of the triangle = 8 cm.

Side BC lies on the line x = 4 or it is parallel to y-axis. Therefore the height of the triangle will be parallel to x axis. In order to minimize the distance of point A from the origin, point A should lie on the x-axis as shown.

Hence, point A is at a distance of 8 units from x = 4 and lies on x-axis.

Therefore point A is (-4,0) and the distance of point A from the origin = 4 units.

Hence, option (b).

Answer: Option A

Explanation :

The triangle formed by joining the endpoints of the chord of a circle with the center of the circle is an isosceles triangle because the two sides of the triangle (radii of the circle) are congruent. If the angle subtended by the chord at the center of the circle is 60 degrees, the triangle is an equilateral triangle. Therefore the side of the triangle and the radius of the circle is equal to the side of the triangle = 5 cm.

Now we have the following

OP is perpendicular to the chord AB. Therefore P is the midpoint of chord AB. Further, OA and OP are the radii of the circle. Therefore triangles OAP and OBP are congruent. Therefore triangle OAP and OBP are 30-60-90 triangles.

We have, $\cos 30=\frac{\sqrt{3}}{2}=\frac{AP}{OA}=\frac{AP}{5}$

Therefore, $AP=\frac{5}{2}\sqrt{3}$

Therefore, $\mathcal{l}\left(AB\right)=2\times \mathcal{l}\left(AP\right)=5\sqrt{3}$

Hence, option (a).

Answer: Option B

Explanation :

 
Area of parallelogram = Base × Height

∴ 48 = 8 × Height

∴ Height = 6 cm

If the parallelogram is a rectangle, AD is its height. In that case, s = 6.

Otherwise, using Pythagoras theorem,

AD > 6 or s > 6.

Therefore, s ≥ 6.

Hence, option (b).

Answer: Option C

Explanation :

Suppose l = length of the rectangle and b = breadth of the rectangle.

Therefore, the area of the rectangle = lb and the perimeter of the rectangle = 2(l + b)

Therefore,

$\frac{\mathcal{l}b}{{\left[2\right(l+b\left)\right]}^2}=\frac{1}{25} i.e. \frac{\iota b}{{(l+b)}^2}=\frac{4}{25}$

Substituting the options, we can see that only option (c) i.e., 1 : 4 matches.

Hence, option (c).

Answer: Option A

Explanation :

The area of the semicircle = 72π sq. cm. If ‘r’ is the radius of the semi-circular portion removed,

We get $\pi \times \frac{r^2}{2}=72$

Therefore r = 12 cm.
Therefore the diameter of the semi-circle = AB = 24 cm.

Area of rectangle ABCD = 768 sq. cm.

Therefore the length of side AC $=\frac{768}{24}=32 cm.$

The perimeter of the leftover portion

= Perimeter of the semicircle + l(AD) + l(DC) + l(CB)
= 12π + 32 + 24 + 32 = 88 + 12π

Hence, option (a).

Answer: 24

Explanation :

Since points P and Q lie on the circumference of the circle drawn with BC as diameter, angles BPC and BQC are right angled triangles.

Now, area of triangle ABC = $\frac{1}{2}\times AB\times PC$ = $\frac{1}{2}\times AC\times BQ$

Therefore, BQ = $\frac{\mathrm{AB}\times \mathrm{PC}}{\mathrm{AC}}$ = $\frac{30\times 20}{25}$ = 24

Hence, 24.

Answer: Option A

Explanation :

Given, p³ = q⁴ = r⁵ = s⁶ = k

⇒ p³ = k
⇒ p = k^1/3

Similarly,
q = k^1/4
r = k^1/5
s = k^1/6

pqr = k^1/3 × k^1/4 × k^1/5 = k^{1/3 + 1/4 + 1/5} = k^47/60

Now, log_s(pqr) = log_k^1/6 k^47/60 = 47/10

Hence, option (a).

Answer: Option C

Explanation :

We have, 4ⁿ > 17¹⁹

Taking log on both sides to the base 4,
 
n × log₄ 4 > 19 × log₄ 17

Now, 17 > 4^2.

∴ log₄ 17 > 2.

⇒ n × log₄ 4 > 19 × log₄ 17 > 19 × 2

Also, log₄ 4 = 1

∴ n > 38.

Hence, option (c).

Answer: Option D

Explanation :

$\frac{1}{l{\mathrm{og}}_{2}100}$ - $\frac{1}{{\log }_{4}100}$ + $\frac{1}{{\log }_{5}100}$ - $\frac{1}{{\log }_{10}100}$ + $\frac{1}{{\log }_{20}100}$ - $\frac{1}{{\log }_{25}100}$ + $\frac{1}{{\log }_{50}100}$

= ${\log }_{100}2$ - ${\log }_{100}4$ + ${\log }_{100}5$ - ${\log }_{100}10$ + ${\log }_{100}20$ - ${\log }_{100}25$ + ${\log }_{100}50$

= ${\log }_{100}\left(\frac{2\times 5\times 20\times 50}{4\times 10\times 25}\right)$ = ${\log }_{100}\left(10\right)$ = $\frac{1}{2}$

Hence, option (d).

Answer: Option D

Explanation :

Given: a² + b² = 97.

AM ≥ GM

⇒ $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2}{2}$ ≥ $\sqrt{{\mathrm{a}}^2\times {\mathrm{b}}^2}$

⇒ 48.5 ≥ |a × b|

⇒ 48.5 ≥ a × b ≥ -48.5

Out of the given options, 64 definitely lies outside this range.

Hence, option (d).

Answer: Option A

Explanation :

Let the original number be 'xy' = 10x + y and
the number formed by reversing the digits = 'yx' = 10y + x. 

We have the following:

10x + y > 3(10y + x)

∴ x > $\frac{29}{7}y$

When y = 1, x = 5, 6, 7, 8 or 9 (Total 5 values)

When y = 2, x = 9 (Total 1 value)

If y > 3, x has to be a 2 digit number which is not possible.

∴ The required answer is 5 + 1 = 6.

Hence, option (a).

Answer: 10

Explanation :

From observation, N^N = 2¹⁶⁰ = 32³² or N = 32.

Now, N² + 2^N = 32² + 2³² = (2⁵ )² + 2³²

= 2¹⁰ + 2³² = 2¹⁰ (1 + 2²² ).

Here, (1 + 2²² ) is an odd number, hence the higest power of 2 is 10.

Therefore the largest value of x = 10.

Hence, 10.

Answer: 36

Explanation :

We have to maximize the value of 2a - 6b. Therefore let us look for the largest possible value of a and the smallest possible value of b.

If 2x² – ax + 2 > 0 for all value of x, the graph of 2x² – ax + 2 is above the x-axis or the roots of the quadratic equations 2x² – ax + 2 = 0 are imaginary or its discriminant is less than 0.
∴ We have a² – 16 < 0 or a² < 16 or –4 < a < 4.
⇒ The largest possible value of a is 3.

If x² – bx + 8 ≥ 0, the discriminant of the equation is less than or equal to zero.
⇒ b² - 32 ≤ 0 
⇒ -4√2 ≤ b ≤ 4√2
⇒ -5.64 ≤ b ≤ 5.64
∴ The smallest possible value of b is –5.

Therefore the maximum possible value of 2a - 6b = 2(3) – 6(–5) = 36.

Hence, 36.

Answer: 8

Explanation :

The sum of the coefficients of n³ -11n² + 32n - 28 is not zero.

Similarly the sum of the odd coefficients of n³ -11n² + 32n - 28 is not equal to its even coefficients. Therefore it is not divisible by (n - 1) and (n + 1).

If we put n = 2, n³ – 11n² + 32n – 28 = 8 – 44 + 64 – 28 = 0.
 
Therefore (n – 2) is a factor of the polynomial n³ - 11n² + 32n – 28.

We have, (n - 2) is a factor of n³ – 11n² + 32n – 28

∴ n³ – 11n² + 32n – 28 = (n - 2)(n² – 9n + 14) = (n – 2)(n – 2)(n - 7) = (n – 2)² (n – 7).

Now, we have (n – 2)² (n – 7) > 0

(n - 2)² is always greater than 0, when n > 2.

⇒ For (n – 2)² (n – 7) > 0, (n - 7) should be greater than 0.

⇒ n > 7.

​​​​​​​Therefore the smallest integer for which n³ - 11n² + 32n - 28 > 0 is 8.

Hence, 8.

Answer: 1098

Explanation :

The number of matches played in a group of ‘n’ peope = ​​$\frac{\mathrm{n}(\mathrm{n}-1)}{2}$

The number of girl vs girl matches in junior level = 153.

Therefore, $\frac{\mathrm{n}(\mathrm{n}-1)}{2}$ = 153 ⇒ n = 18

Therefore there are 18 girls at junior level.
⇒ There are 43 - 18 = 25 boys at junior level.

The number of boy vs boy matches in senior level = 276.
Therefore, $\frac{\mathrm{n}(\mathrm{n}-1)}{2}$ = 276 ⇒ n = 24

Therefore there are 24 boys at senior level.
⇒ There are 51 - 24 = 27 girls at senior level.

Therefore, we have

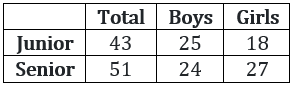
Therefore, the number of boys vs girls matches = 25 × 18 + 24 × 27 = 1098

Hence, 1098.

Answer: 24

Explanation :

S_k = 2k² + 9k + 13

S_k-1 = 2(k-1)² + 9(k-1) + 13

⇒ T_k = S_k - S_k-1 = 2k² + 9k + 13 - [2(k-1)² + 9(k-1) + 13]

⇒ T_k = S_k - S_k-1 = 4k + 7

If t_k = 103

⇒ 4k + 7 = 103 or k = 24.

Hence, 24.

Answer: 20

Explanation :

The graph of the function 52 – 2x² will be of ‘inverted U’ shape, while the graph of the function y = 5x will be a straight line with a positive slope.

Therefore, the minimum value of the required function will be obtained at a point of intersection of y = 52 – 2x² and y = 5x.

Therefore, 52 – 2x² = 5x or 2x² + 5x – 52 = 0.

∴ (x - 4)(2x + 13) = 0

∴ x = 4 or x = $-\frac{13}{2}$

Since x is a positive real number, x = 4.

At x = 4, 5x = 52 – 2x² = 20

Hence, 20.

Answer: Option D

Explanation :

The first number in the terms are 7, 11, 15, …, 95, which form an AP with a = 7 and d = 4.

The n^th term for this AP is T_n = 3 + 4n and the number of terms is

n = $\frac{95-7}{4}$ + 1 = 23

The second number in the terms are 11,15,19,...,99, which form an AP with a = 11 and d = 4. The nth term for this AP is Tn= 7 + 4n and the number of terms is
n = $\frac{99-11}{4}$ + 1 = 23

Therefore the required sum
= $\sum _{n=1}^{23}(3+4n)(7+4n)$

 = $\sum _{n=1}^{23}(16n^2+40n+21)$

= $16\sum _{n=1}^{23}{n}^2+40\sum _{n=1}^{23}n+21\sum _{n=1}^{23}1$

= $16\times \frac{23\times 24\times 47}{6}+40\times \frac{23\times 24}{2}+21\times 23$

= 69184 + 11040 + 483

= 80707

Hence, option (d).

Answer: Option A

Explanation :

For n = 1, A₁ = 0

For n = 2, A₂ = 1225 = 35 × 35

Also, 6²ⁿ- 35n - 1 = (36ⁿ - 1) - 35n.

The term in the bracket 36ⁿ - 1 is always divisible by (36 - 1) or by 35. Similarly 35n is also always divisible by 35. Therefore each term in the set A is divisible by 35. However, not all positive multiples of 35 are present in set A.

For n = 1, B₁ = 35(1 - 1) = 0

For n = 2, B₂ = 35(2 - 1) = 35 and so on.

Thus all whole number multiples of 35 are present in set B.

Thus every member of set A is present in every member of set B but at least one member of set B is not present in set A.

Hence, option (a).

Answer: Option D

Explanation :

The set (PΔQ) = {1,4,5,6}.

The set (RΔS) = {1,2,3,4,7,8,10}

Therefore the set (PΔQ) Δ (RΔS) = {2,3,5,6,7,8,10}.

Thus there are 7 elements in the set.

Hence, option (d).