CAT 2003 QA - Leaked | Previous Year CAT Paper
Join our Telegram Group for CAT Preparation.
Answer the following question based on the information given below.
A certain perfume is available at a duty-free shop at the Bangkok international airport. It is priced in the Thai currency Baht but other currencies are also acceptable. In particular, the shop accepts Euro and US Dollar at the following rates of exchange:
US Dollar 1 = 41 Bahts and Euro 1 = 46 Bahts
The perfume is priced at 520 Bahts per bottle. After one bottle is purchased, subsequent bottles are available at a discount of 30%. Three friends S, R and M together purchase three bottles of the perfume, agreeing to share the cost equally. R pays 2 Euros. M pays 4 Euros and 27 Thai Bahts and S pays the remaining amount in US Dollars.
How much does R owe to S in Thai Baht?
- A.
428
- B.
416
- C.
334
- D.
324
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Price of 1st bottle = 520 Bahts
Price of 2nd and 3rd bottles each = (520 × 0.7) = 364 Bahts
∴ Total cost of all three bottles = 1248 Bahts
Cost per person = 416 Bahts
R pays 2 Euros = 2 × 46 = 92 Bahts
M pays 4 Euros and 27 Bahts = 4 × 46 + 27 = 211 Bahts
S pays the remaining amount = 1248 − (92 + 211) = 945 Bahts
∴ R owes 416 − 92 = 324 Bahts to S.
Hence, option (d).
Workspace:
How much does M owe to S in US Dollars?
- A.
3
- B.
4
- C.
5
- D.
6
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Price of 1st bottle = 520 Bahts
Price of 2nd and 3rd bottles each = (520 × 0.7) = 364 Bahts
∴ Total cost of all three bottles = 1248 Bahts
Cost per person = 416 Bahts
R pays 2 Euros = 2 × 46 = 92 Bahts
M pays 4 Euros and 27 Bahts = 4 × 46 + 27 = 211 Bahts
S pays the remaining amount = 1248 − (92 + 211) = 945 Bahts
M owes = 416 − 211 = 205 Bahts to S
But, 205 Bahts = 205/41 = 5 US Dollars
Hence, option (c).
Workspace:
Answer the following question based on the information given below.
New Age Consultants have three consultants Gyani, Medha and Buddhi. The sum of the number of projects handled by Gyani and Buddhi individually is equal to the number of projects in which Medha is involved. All three consultants are involved together in 6 projects. Gyani works with Medha in 14 projects. Buddhi has 2 projects with Medha but without Gyani and 3 projects with Gyani but without Medha. The total number of projects for New Age Consultants is one less than twice the number of projects in which more than one consultant is involved.
What is the number of projects in which Gyani alone is involved?
- A.
Uniquely equal to zero
- B.
Uniquely equal to 1
- C.
Uniquely equal to 4
- D.
Cannot be determined uniquely
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :

Let a be the number of projects in which only Gyani is involved, g be the number of projects in which only Buddhi is involved and c be the number of projects in which only Medha is involved.
From the data, d = 6
b + d = 14
∴ b = 8
Also, e = 3 and f = 2
It is given that
a + g = b + c + d + f
∴ a − c + g = 16 … (i)
Number of projects involving more than 1 consultant = 6 + 8 + 2 + 3 = 19
∴ Total number of projects = 2 × 19 − 1 = 37
a + b + c + d + e + f + g = 2 × (b + d + e + f) − 1
∴ a + c + g = 19 − 1 = 18 … (ii)
Solving (i) and (ii), we get,
c = 1 and a + g = 17
∴ a cannot be determined uniquely.
Hence, option (d).
Workspace:
What is the number of projects in which Medha alone is involved?
- A.
Uniquely equal to zero
- B.
Uniquely equal to 1
- C.
Uniquely equal to 4
- D.
Cannot be determined uniquely
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :

Let a be the number of projects in which only Gyani is involved, g be the number of projects in which only Buddhi is involved and c be the number of projects in which only Medha is involved.
From the data, d = 6
b + d = 14
∴ b = 8
Also, e = 3 and f = 2
It is given that
a + g = b + c + d + f
∴ a − c + g = 16 … (i)
Number of projects involving more than 1 consultant = 6 + 8 + 2 + 3 = 19
∴ Total number of projects = 2 × 19 − 1 = 37
a + b + c + d + e + f + g = 2 × (b + d + e + f) − 1
∴ a + c + g = 19 − 1 = 18 … (ii)
Solving (i) and (ii), we get,
c = 1 and a + g = 17
we get, c = 1
∴ Number of projects in which Medha alone is involved = 1
Hence, option (b).
Workspace:
The number of non-negative real roots of 2x – x – 1 = 0 equals
- A.
0
- B.
1
- C.
2
- D.
3
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
2x − x − 1 = 0
∴ 2x = x + 1
This equation indicates the intersection of an exponential curve, lying in the I and II quadrants, and a straight line.
∴ It can have two intersection points at the most.
In this case, we can find two intersection points by trial and error as x = 0 and x = 1
∴ There cannot be any other point of intersection.
∴ The equation has 2 non-negative real roots.
Hence, option (c).
Workspace:
When the curves, y = log10 x and y = x−1 are drawn in the X-Y plane, how many times do they intersect for values of x ≥ 1?
- A.
Never
- B.
Once
- C.
Twice
- D.
More than twice
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :

As shown in the above figure, the graphs for, y = 1/x and y = log10 x intersect at only one point.
Hence, option (b).
Alternatively,
To find the point of intersection, we just equate these two functions.
1/x = log10 x
Putting y = 1/x, we get,
10y = 1/y
Here, R.H.S. (i.e. 1/y) cannot be negative as L.H.S. (10y) cannot be negative.
For y = 0, L.H.S. < R.H.S.
for y = 1, L.H.S. > R.H.S.
From this we understand that these two functions intersect each other at least once.
But, 10y is an increasing function and 1/y is a decreasing function.
∴ They intersect each other at a single point only.
Hence, option (b).
Workspace:
Let A and B be two solid spheres such that the surface area of B is 300% higher than the surface area of A. The volume of A is found to be k% lower than the volume of B. The value of k must be
- A.
85.5
- B.
92.5
- C.
90.5
- D.
87.5
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Ratio of areas of two spheres = s1 : s2 = 4 : 1
∴ Ratio of their radii = r1 : r2 = 2 : 1
∴ Ratio of their volumes = v1 : v2 = 8 : 1
Volume of A is 12.5% (1/8th) of the volume of B.
But, volume of A is k% less than B.
∴ k = (100 − 12.5) = 87.5%
Hence, option (d).
Workspace:
Which one of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0?
x + 2y − 3z = p
2x + 6y − 11z = q
x − 2y + 7z = r
- A.
5p − 2q − r = 0
- B.
5p + 2q + r = 0
- C.
5p + 2q − r = 0
- D.
5p − 2q + r = 0
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
On substituting the values of p, q and r in the options we see that the values of p, q and r satisfy only the equation 5p − 2q − r = 0.
Hence, option (a).
Alternatively,
In order to understand this solution we need to have an understanding of a few concepts of higher mathematics like “Rank of a matrix”.
A number p is said to be the rank of a matrix A if
(i) A possesses at least one p-rowed determinant whose value is not zero
(ii) A does not possess any non zero (p + 1) rowed determinant.
In other words, the number of non-zero rows in the row-reduced form of a matrix is called the rank of a matrix.
For example,
Consider the matrix,
Matrix A has only one 3 rowed determinant, namely
The value of this determinant is zero. Hence, the rank of A will be less than 3.
Now we will try to find a 2 rowed non zero determinant.
= 42 - 5.1 = 3 ≠ 0
The fact that every 3 rowed determinant of A is zero and there is at least one 2 rowed determinant of A which is not zero, is generally expressed by saying that the rank of A is 2.
Consider the system of equations,
x + 2y − 3z = p
2x + 6y − 11z = q
x − 2y + 7z = r
The coefficient matrix (whose elements are coefficients of the three unknowns x, y and z) of the system is
And the Augmented matrix is
For the system of equations to possess solutions it is necessary that the rank of the augmented matrix and the rank of the coefficient matrix should be equal.
Let us first find the rank of the coefficient matrix.
We will first find the value of the only 3 rowed determinant of A,
= 1(6 × 7 - 11 × (-2)) - 2(2 × 7 - (-11)1) - 3(2 × (-2) - 6 × 1) = 0
Hence, the rank of the coefficient matrix will be less than 3.
The following is a two-rowed non-zero determinant in the coefficient matrix
= 6 - 4 = 2 ≠ 0
Hence, the rank of the coefficient matrix is 2.
For the system of equations to possess solutions the rank of the augmented matrix should also be 2.
We will first try to simplify the augmented matrix using row operations.
By the row operation R3 → R3 - R1
we reduce the augmented matrix to the equivalent matrix,
(By the row operation R2 → R2 - 2R1)
(By the row operation R3 → R3 - 2R2)
For the augmented matrix to have rank 2 every 3 rowed determinant should be zero.
Hence,
5p − 2q − r = 0
Hence, option (a).
Workspace:
A leather factory produces two kinds of bags, standard and deluxe. The profit margin is Rs. 20 on a standard bag and Rs. 30 on a deluxe bag. Every bag must be processed on machine A and on machine B. The processing times per bag on the two machines are as follows:
The total time available on machine A is 700 hours and on machine B is 1250 hours. Among the following production plans, which one meets the machine availability constraints and maximizes the profit?

- A.
Standard 75 bags, Deluxe 80 bags
- B.
Standard 100 bags, Deluxe 60 bags
- C.
Standard 50 bags, Deluxe 100 bags
- D.
Standard 60 bags, Deluxe 90 bags
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
Total time available is 700 hrs on machine A and 1250 hrs on machine B.
Let the number of Standard Bags be s and the number of Deluxe Bags be d.
Here we have to maximize the profit margin i.e. 20s + 30d, subject to the constraints,
4s + 5d ≤ 700 and 6s + 10d ≤ 1250
Now consider options.
1. s = 75 and d = 80
∴ The profit = 75 × 20 + 30 × 80 = 3900
4s + 5d = 700 and 6s + 10d = 1250
∴ the constraints are satisfied.
2. s = 100 and d = 60
∴ The profit = 100 × 20 + 60 × 30 = 3800
The profit is less than in option 1.
∴ Option 2 is not the answer.
3. s = 50 and d = 100
∴ The profit = 50 × 20 + 100 × 30 = 4000
4s + 5d = 700 and 6s + 10d = 1300
∴ The second constraint is not satisfied.
∴ Option 3 cannot be the answer.
4. s = 60 and d = 90
∴ The profit = 60 × 20 + 90 × 30 = 3900
4s + 5d = 690 and 6s + 10d = 1260
∴ The second constraint is not satisfied.
∴ Option 4 cannot be the answer.
As only option 1 satisfies the constraints and also maximizes the profit, option 1 is the answer.
Hence, option (a).
Workspace:
The sum of 3rd and 15th elements of an arithmetic progression is equal to the sum of 6th, 11th and 13th elements of the same progression. Then which element of the series should necessarily be equal to zero?
- A.
1st
- B.
9th
- C.
12th
- D.
None of the above
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Assume that the first term of the progression is a and the common difference is d.
∵ T3 + T15 = T6 + T11 + T13
∴ (a + 2d) + (a + 14d) = (a + 5d) + (a + 10d) + (a + 12d)
∴ a + 11d = 0
But, T12 = a + 11d
∴ The 12th term of an arithmetic progression is 0.
Hence, option (c).
Workspace:
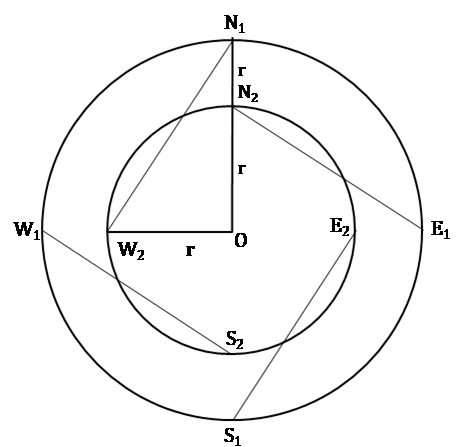
Answer the following question based on the information given below.
A city has two perfectly circular and concentric ring roads, the outer ring road (OR) being twice as long as the inner ring road (IR). There are also four (straight line) chord roads from E1, the east end point of OR to N2, the north end point of IR; from N1, the north end point of OR to W2, the west end point of IR; from W1, the west end point of OR, to S2, the south end point of IR; and from S1, the south end point of OR to E2, the east endpoint of IR. Traffic moves at a constant speed of 30π km/hr on the OR road, 20π km/hr on the IR road, and km/hr on all the chord roads.
The ratio of the sum of the lengths of all chord roads to the length of the outer ring road is
- A.
- B.
- C.
- D.
None of the above
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the diagram below as per the conditions given in the question,
Speed on outer ring road = 30π km/hr
Speed on inner ring road = 20π km/hr
And speed on chord roads = km/hr
Let R and r be radii of the Outer Ring road and the Inner Ring road respectively.
∵ Outer Ring road is twice as long as Inner Ring road, we have,
∴ 2πR = 2 × (2πr)
∴ R = 2r
∴ Length of inner ring road = 2πr km and outer ring road = 4πr km
In the figure above, in ∆OW2N1,
W2N1 = km
∴ Length of the chord road = km
∴ Ratio of the length of all chord roads to length of the outer ring road =
Hence, option (c).
Workspace:
Amit wants to reach N2 from S1. It would take him 90 minutes if he goes on minor arc S1 - E1 on OR, and then on the chord road E1 - N2. What is the radius of the outer ring road in km?
- A.
60
- B.
40
- C.
30
- D.
20
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Total distance to be travelled =
S1–E1 arc of the Outer Ring road + Chord E1 – N2
Given the speeds,
Total time required to travel from S1 to N1 =
∴ r = 15 km
∴ Radius of the Outer Ring road R = 2r = 30 km
Hence, option (c).
Workspace:
Amit wants to reach E2 from N1 using first the chord N1 – W2 and then the inner ring road. What will be his travel time in minutes on the basis of information given in the above question?
- A.
60
- B.
45
- C.
90
- D.
105
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Total distance to be travelled, chord N1– W2 + W2– E2 arc of the Inner Ring road
Given the speeds,
Total time required to travel from N1 to E2 =
= 105 minutes
Hence, option (d).
Workspace:
A test has 50 questions. A student scores 1 mark for a correct answer, −1/3 for a wrong answer, and −1/6 for not attempting a question. If the net score of a student is 32, the number of questions answered wrongly by that student cannot be less than
- A.
6
- B.
12
- C.
3
- D.
9
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Let R, W and N be the number of questions with right answers, questions with wrong answers and not attempted questions respectively.
From the conditions given in the question, we have,
R + W + N = 50 … (i)
R − W/3 − N/6 = 32 … (ii)
Solving equations (i) and (ii), we get,
7R − 242 = W
∴ W will be minimum for R = 35, i.e. W = 3
Hence, option (c).
Workspace:
Twenty-seven persons attend a party. Which one of the following statements can never be true?
- A.
There is a person in the party who is acquainted with all the twenty-six others.
- B.
Each person in the party has a different number of acquaintances.
- C.
There is a person in the party who has an odd number of acquaintances.
- D.
In the party, there is no set of three mutual acquaintances.
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Consider option 1: There may be a person in the party who is acquainted with all the twenty-six others and rest may have the same or different number of acquaintances.
Consider option 2: For all people to have a different number of acquaintances, the first person will have a maximum of 26 acquaintances, the second person will have 25 acquaintances and so on. Continuing in this manner, the last person will have 0 acquaintances, which is not possible.
Consider option 3: There may be a person in the party who has an odd number of acquaintances.
Consider option 4: In the case that none of the people attending the party know each other, then option 4 will be true, and hence it is not the correct option.
Hence, option (b).
Workspace:
Let g(x) = max(5 − x, x + 2). The smallest possible value of g(x) is
- A.
4.0
- B.
4.5
- C.
1.5
- D.
None of the above
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
We have, g(x) = max(5 − x, x + 2)
We have to find the smallest value of g(x).
The lines y = 5 – x and y = x + 2 intersect each other at the point (1.5, 3.5)
For x < 1.5, 5 – x > x + 2 and 5 – x > 3.5
For x > 1.5, x + 2 > 5 – x and x + 2 > 3.5
∴ At any point other than x = 1.5, the value of g(x) is greater than 3.5
Thus the smallest possible value of g(x) = 3.5 at x = 1.5
Hence, option (d).
Workspace:
The function f(x) = |x − 2| + |2.5 − x| + |3.6 − x|, where x is a real number, attains a minimum at
- A.
x = 2.3
- B.
x = 2.5
- C.
x = 2.7
- D.
None of the above
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
f(x) = |x − 2| + |2.5 − x| + |3.6 − x| = g(x) + |2.5 – x|, where g(x) = |x − 2| + |3.6 − x|
When 2 ≤ x ≤ 3.6, g(x) attains a fixed value.
This happens as in this range |x – 2| = x – 2 and |3.6 – x| = 3.6 – x
∴ |x − 2| + |3.6 − x| = x – 2 + 3.6 – x = 1.6
When x < 2, x – 2 < 0, |x – 2| > 0
Also, as –x > –2, 3.6 – x > 3.6 – 2
∴ 3.6 – x > 1.6
∴ |x − 2| + |3.6 − x| > 1.6
Similarly, when x > 3.6,
|3.6 – x| > 0 and |x – 2| > 1.6
∴ |x − 2| + |3.6 − x| > 1.6
Thus we can say that g(x) has the minimum value in the range 2 ≤ x ≤ 3.6
As f(x) = g(x) + |2.5 – x|,
∴ f(x) attains the minimum value when 2 ≤ x ≤ 3.6 and |2.5 – x| is minimum.
This happens when x = 2.5
∴ f(x) attains minimum when x = 2.5
Hence, option (b).
Alternatively,
f(x) = |x − 2| + |2.5 − x| + |3.6 − x|
Substituting the value of x from the given options in the function,
when x = 2.3
f(x) = 0.3 + 0.2 + 1.3 = 1.8
when x = 2.5
f(x) = 0.5 + 0 + 1.1 = 1.6
when x = 2.7
f(x) = 0.7 + 0.2 + 0.9 = 1.8
Substituting any arbitrary real values of x in f(x),
when x = 2
f(x) = 0 + 0.5 + 1.6 = 2.1
when x = 3
f(x) = 1 + 0.5 + 0.6 = 2.1
For any other value of x, f(x) will be greater than 1.6
Hence, f(x) is minimum when x = 2.5
Hence, option (b).
Workspace:
How many even integers n, where 100 ≤ n ≤ 200, are divisible neither by seven nor by nine?
- A.
40
- B.
37
- C.
39
- D.
38
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Number of even integers satisfying inequality i.e. 100 ≤ n ≤ 200 = 51
Total even integers divisible by 7 = 112, 126, 140, 154, 168, 182, 196 = 7
Total even integers divisible by 9 = 108, 126, 144, 162, 180, 198 = 6
The number 126 is repeated in both the sets.
∴ Total number of positive even numbers between 100 and 200 which are either divisible by 7 or 9 = 7 + 6 − 1 = 12
∴ Total number of positive even numbers between 100 and 200 which are divisible neither by 7 nor by 9 = 51 − 12 = 39
Hence, option (c).
Workspace:
A positive whole number M less than 100 is represented in base 2 notation, base 3 notation, and base 5 notation. It is found that in all three cases the last digit is 1, while in exactly two out of the three cases the leading digit is 1. Then M equals
- A.
31
- B.
63
- C.
75
- D.
91
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Of the four given options 63 and 75 are multiples of 3. Their remainder cannot be 1.
∴ The last digit cannot be 1. Thus, 63 and 75 are eliminated.
For the options 31 and 91, the remainder is 1. Thus, the last digit is 1.
31 = (11111)2 = (1011)3 = (111)5
91 = (1011011)2 = (10101)3 = (331)5
91 has 1 as the first digit in only 2 of the notations.
Hence, option (d).
Workspace:
In a 4000 meter race around a circular stadium having a circumference of 1000 meters, the fastest runner and the slowest runner reach the same point at the end of the 5th minute, for the first time after the start of the race. All the runners have the same starting point and each runner maintains a uniform speed throughout the race. If the fastest runner runs at twice the speed of the slowest runner, what is the time taken by the fastest runner to finish the race?
- A.
20 min
- B.
15 min
- C.
10 min
- D.
5 min
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Let the speed of the slowest runner be s m/min and the speed of the fastest runner be 2s m/min.
Length of the race track = 1000 m and the two runners meet after 5 minutes.
∴ Relative speed = 1000/5 = 200 m/min
∴ 2s − s = 200
∴ s = 200 m/min
∴ The speed of the fastest runner = 2s = 400 m/min
∴ The time taken by the fastest runner to complete the race = 4000/400 = 10 min
Hence, option (c).
Alternatively,
The slowest runner covers 500 m when the fastest runner covers 1000 m.
∴ The two meet at the starting point when the fastest runner covers 2000 m and the slowest runner covers 1000 m.
∴ The fastest runner runs 2000 m in 5 minutes.
∴ He runs 4000 m in 10 minutes.
Hence, option (c).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Is a44 < b11, given that a = 2 and b is an integer?
- b is even
- b is greater than 16
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
a44 < b11
But, a = 2
∴ a44 = 244
∴ a44 = 1611
Using statement 1 alone:
b is an even integer. It may be less than or greater than 16.
So, we cannot answer the question using statement 1 alone.
Using statement 2 alone:
b is greater than 16.
∴ b11 > 1611
∴ b11 > a44
So, we can answer the question using statement 2 alone.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
What are the unique values of b and c in the equation 4x2 + bx + c = 0 if one of the roots of the equation is (−1/2)?
A. The second root is 1/2
B. The ratio of c and b is 1
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
4x2 + bx + c = 0 …(i)
One root = −1/2
Using statement A alone:
Second root is 1/2.
Sum of the roots = −b/4 = (−1/2) + 1/2 = 0
∴ b = 0
Also, product of the roots = c/4 = (−1/2) × (1/2) = (−1/4)
∴ c = −1
So, statement A alone is sufficient to answer the question.
Using statement B alone:
Ratio of c and b is 1.
∴ b = c
∴ Equation (i) becomes 4x2 + bx + b = 0 ...(ii)
But one root = −1/2
Substituting x = −1/2 in the above equation (ii), we get,
1 − b/2 + b = 0
∴ b = −2 and c = −2
So, statement B alone is also sufficient to answer the question.
Hence, option (b).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
AB is a chord of a circle. AB = 5 cm. A tangent parallel to AB touches the minor arc AB at E. What is the radius of the circle?
A. AB is not a diameter of the circle
B. The distance between AB and the tangent at E is 5 cm
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
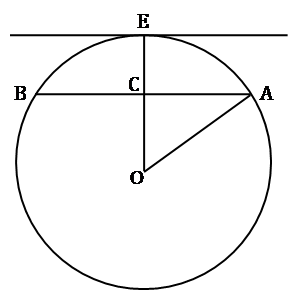
Let radius of circle be r.
AC = 2.5 as radius bisects the chord.
Using statement A alone:
We have been told that AB is not a diameter of the circle. But it does not give us any useful information to solve the problem.
So, statement A alone is not sufficient to answer the question.
Using statement B alone:
From the figure above, CE = 5
∴ OC = r − 5
∴ OA2 = OC2 + AC2
∴ r2 = (r − 5)2 + (2.5)2
Solving the above equation,
r = 3.125 cm
So, statement B alone is sufficient to answer the question.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
Is
A. −3 ≤ a ≤ 3
B. One of the roots of the equation 4x2 − 4x + 1 = 0 is a
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
R.H.S. and L.H.S. are infinite GP's with common ratio = .
∴ We need to find whether
...(i)
This statement (i) is always true for a < 1.
Using statement A alone:
It does not give any conclusion regarding value of a i.e. whether it is less than 1 or not.
So, statement A alone is not sufficient to answer the question.
Using statement B alone:
4a2 − 4a + 1 = 0 …(ii)
∴ a = 1/2
So, statement B alone is sufficient to answer the question.
Hence, option (a).
Workspace:
Each question is followed by two statements, A and B. Answer each question using the following instructions
Choose 1 if the question can be answered by using one of the statements alone but not by using the other statement alone.
Choose 2 if the question can be answered by using either of the statements alone.
Choose 3 if the question can be answered by using both statements together but not by either statement alone.
Choose 4 if the question cannot be answered on the basis of the two statements.
D, E, F are the mid-points of the sides AB, BC and CA of triangle ABC respectively. What is the area of DEF in square centimetres?
A. AD = 1 cm, DF = 1 cm and perimeter of DEF = 3 cm
B. Perimeter of ABC = 6 cm, AB = 2 cm, and AC = 2 cm
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
D, E and F are the midpoints of AB, BC and CA respectively.
Using statement A alone:
∵ AD = 1 cm
∴ BD = 1 cm …(Since D is the mid-point)
∵ DF = 1 cm
∴ BC = 2 cm …(Since D and F are the mid-points and DF is parallel to BC)
∴ BE = 1 cm and EC = 1 cm
∵ Perimeter of DEF = 3 cm
∴ EF = 1 cm
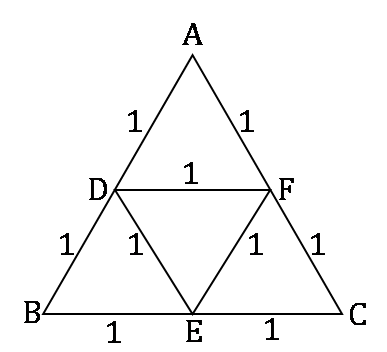
∴ Area of ∆DEF can be obtained.
So, statement A alone is sufficient to obtain the answer.
Using statement B alone:
∵ Perimeter of ∆ABC = 6 cm, AB = 2 cm, AC = 2 cm
∴ BC = 2 cm
∴ DE = 1, EF = 1 and DF = 1

So, statement B alone is also sufficient to obtain the answer.
Hence, option (b).
Workspace:
At the end of year 1998, Shepard bought nine dozen goats. Henceforth, every year he added p% of the goats at the beginning of the year and sold q% of the goats at the end of the year where p > 0 and q > 0. If Shepard had nine dozen goats at the end of year 2002, after making the sales for that year, which of the following is true?
- A.
p = q
- B.
p < q
- C.
p > q
- D.
p = q/2
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Shepard bought 9 dozen goats at the end of 1998.
Consider that he added 1 dozen goats to it, i.e. 11.11% of 9 dozen.
And he sold 1 dozen to get back the same 9 dozen i.e. 10% of 10 dozen.
∴ He adds 11.11% and subtracts 10% to get the same amount every time.
∴ p = 11.11% and q = 10%
∴ p > q
Hence, option (c).
Workspace:
Each side of a given polygon is parallel to either the X or the Y axis. A corner of such a polygon is said to be convex if the internal angle is 90° or concave if the internal angle is 270°. If the number of convex corners in such a polygon is 25, the number of concave corners must be
- A.
20
- B.
0
- C.
21
- D.
22
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :

Consider the polygon as shown in the figure. Here 4 corners A, D, G and J are the concave corners and remaining 8 corners are convex corners.
In general, for a polygon with sides parallel to either of the axes, if n is the number of concave corners and m is the number of convex corners, then we have,
m − n = 4
∵ m = 25
∴ n = 21
Hence, option (c).
Workspace:
The 288th term of the series a, b, b, c, c, c, d, d, d, d, e, e, e, e, e, f, f, f, f, f, f... is
- A.
u
- B.
v
- C.
w
- D.
x
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
In the series a, b, b, c, c, c, d, d, d, d, e, e, e, e, e,...
the first letter of the alphabet is written once, the second is written twice, and the nth letter is written n times.
∴ The number of letters written upto the nth letter is equal to the sum of the first n natural numbers given by, n(n + 1)/2
For n = 23, n(n + 1)/2 = 276 and for n = 24, n(n + 1)/2 = 300
This means the series contains 276 letters in all for the letter corresponding to n = 23 and 300 letters in all for the letter corresponding to n = 24.
∴ The letter corresponding to n = 24 will be the letter occupying the 277th to the 300th place in the series.
But, n = 24 corresponds to letter x.
∴ The 288th letter in the series is x.
Hence, option (d).
Workspace:
Let p and q be the roots of the quadratic equation x2 − (α − 2)x − α − 1 = 0. What is the minimum possible value of p2 + q2?
- A.
0
- B.
3
- C.
4
- D.
5
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
p2 + q2 = (p + q)2 − 2pq …(i)
From given equation, p + q = α − 2 and pq = − α − 1
Substituting values in equation (i), we get,
p2 + q2 = α2 + 4 − 4α − 2(−α − 1)
= α2 + 4 − 4α + 2α + 2
= α2 − 2α + 1 + 5
= (α − 1)2 + 5
Minimum value of p2 + q2 will be obtained by putting (α − 1) = 0
∴ Minimum value = 5
Hence, option (d).
Workspace:
There are two concentric circles such that the area of the outer circle is four times the area of the inner circle. Let A, B and C be three distinct points on the perimeter of the outer circle such that AB and AC are tangents to the inner circle. If the area of the outer circle is 12 square centimetres then the area (in square centimetres) of the triangle ABC would be
- A.
- B.
- C.
- D.
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the diagram below, as per the given conditions.

Let r and R be the radii of the inner circle and outer circle respectively.
As area of the outer circle is 4 times the area of the inner circle, we have, R = 2r
In ∆OAM, sin θ =
∴ ∠OAM = θ = 30°
Similarly,
∠OAM = ∠OBM = ∠OAC = ∠OCA = 30°
∠OBC = ∠OCB = 30°
∴ ∠BAC = ∠ACB = ∠CBA
∴ ∆ABC is an equilateral triangle.
AB = 2 ×
Area of ∆ABC = × (AB)2 = × 4 × 3 × r2 = ...(i)
But, area of the outer circle = π(2r)2 = 4πr2 = 12
∴ r2 =
∴ Area of ∆ABC =
Hence, option (c).
Workspace:
Let a, b, c, d be four integers such that a + b + c + d = 4m + 1 where m is a positive integer. Given m, which one of the following is necessarily true?
- A.
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 − 2m + 1
- B.
The minimum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
- C.
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 − 2m + 1
- D.
The maximum possible value of a2 + b2 + c2 + d2 is 4m2 + 2m + 1
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
a + b + c + d = 4m + 1
a2 + b2 = (a + b)2 – 2ab
a2 + b2 is minimum when 2ab is maximum.
The product of two numbers is maximum when the numbers are equal.
∴ a² + b² is minimum when a = b
Similarly, c² + d² is minimum when c = d
∴ a² + b² + c² + d² is minimum when a = b and c = d
∴ (a² + b² + c² + d²)min = 2(a² + c²)
But, a² + c² is minimum when a = c
∴ a² + b² + c² + d² is minimum when a = b = c = d
When a = b = c = d, a + b + c + d is a multiple of 4.
But, a + b + c + d = 4m + 1
So, one out of a, b, c, d must be one greater than the other three.
∴ a = b = c = m and d = m + 1
∴ a² + b² + c² + d² = m² + m² + m² + (m + 1)² = 4m² + 2m + 1
Hence, option (b).
Workspace:
Three horses are grazing within a semi-circular field. In the diagram given below, AB is the diameter of the semi-circular field with centre at O. Horses are tied up at P, R and S such that PO and RO are the radii of semi-circles with centres at P and R respectively, and S is the centre of the circle touching the two semi-circles with diameters AO and OB. The horses tied at P and R can graze within the respective semi-circles and the horse tied at S can graze within the circle centred at S. The percentage of the area of the semi-circle with diameter AB that cannot be grazed by the horses is nearest to

- A.
20
- B.
28
- C.
36
- D.
40
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the diagram below.

Let r be the radius of the smaller semi-circles and s be the radius of the smaller circle.
OS = 2r − s
PS = r + s
PO = r
But, ∆PSO is a right-angled triangle.
∴ PS2 = PO2 + SO2
(r + s)2 = r2 + (2r − s)2
∴ r² + s² + 2rs = r² + 4r² + s² − 4rs
∴ Total area not grazed = π(2r)2 -
= 2πr2 - πr2 - πr2
= πr2
∴ Required percentage = × 100
= × 100
≈ 28%
Hence, option (b).
Workspace:
In the figure below, ABCDEF is a regular hexagon and ∠AOF = 90°. FO is parallel to ED. What is the ratio of the area of the triangle AOF to that of the hexagon ABCDEF?

- A.
- B.
- C.
- D.
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
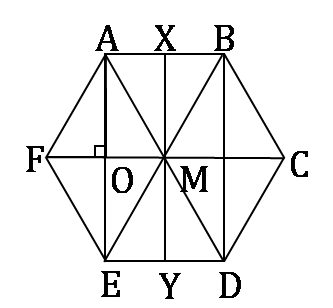
We can see that triangles AMF, AMB, BMC, CMD, DME and EMF are all equilateral triangles. Also, AE, XY and BD bisect MF, AB, ED and CM.
∴ All the small right triangles in the figure are congruent.
∴ A(∆AOF) = × the area of the hexagon ABCDEF
Hence, option (a).
Workspace:
How many three digit positive integers, with digits x, y and z in the hundred's, ten's and unit's place respectively, exist such that x < y, z < y and x ≠ 0?
- A.
245
- B.
285
- C.
240
- D.
320
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
x, y and z are at hundred’s , ten’s and unit's position in a three digit number.
Both x and z have to be less than y.
When y = 9, then x can take values from 1 to 8 and z can take values from 0 to 8.
∴ Total number of ways in which this number can be written when y is 9 = 8 × 9 = 72
The table given below represents the number of ways of writing this number for all possible values of y from 2 to 9.

∴ Total number of ways = 72 + 56 + 42 + 30 + 20 + 12 + 6 + 2 = 240
Hence, option (c).
Workspace:
A vertical tower OP stands at the centre O of a square ABCD. Let h and b denote the lengths OP and AB respectively. Suppose ∠APB = 60°, then the relationship between h and b can be expressed as
- A.
2b2 = h2
- B.
2h2 = b2
- C.
3b2 = 2h2
- D.
3h2 = 2b2
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
OP = h and AB = b
Now, OA =

OP is a perpendicular tower at the centre O of the square.
In ∆PAB, PA = PB
∴ ∠PAB = ∠PBA = ∠APB = 60°
∴ ∆PAB is an equilateral triangle.
∴ AP = b
In the right-angled ∆AOP, we have,
AP2 = OP2 + OA2
∴ b2 = h2 +
∴ 2h2 = b2
Hence, option (b).
Workspace:
In a triangle ABC, AB = 6, BC = 8 and AC = 10. A perpendicular dropped from B, meets the side AC at D. A circle of radius BD (with centre B) is drawn. If the circle cuts AB and BC at P and Q respectively, then AP : QC is equal to
- A.
1 : 1
- B.
3 : 2
- C.
4 : 1
- D.
3 : 8
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
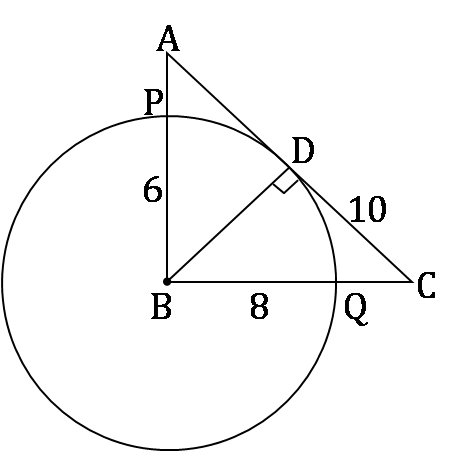
In ∆ABC, AB = 6 cm, BC = 8 and AC = 10
∵ 6, 8, 10 are Pythagorean triplets, ∆ABC is a right triangle.
BD is the perpendicular drawn from B to AC.
∴ A(ΔABC) = 1/2 × 6 × 8 = 1/2 × BD × 10
∴ BD = 4.8 cm
A circle with centre B is drawn which will intersect AB at P and BC at Q.
∴ AP = AB − PB = 1.2 and QC = BC − BQ = 3.2
∴ AP : QC = 3 : 8
Hence, option (d).
Workspace:
In the diagram given below, ∠ABD = ∠CDB = ∠PQD = 90°. If AB : CD = 3 : 1, the ratio of CD : PQ is

- A.
1 : 0.69
- B.
1 : 0.75
- C.
1 : 0.72
- D.
None of the above
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the figure below,

As AB || CD and ∠ABD = ∠CDB = ∠PQD = 90°
∴ ∠BAP = ∠CDP and ∠ABP = ∠DCP
∆CPD ~ ∆BPA …(AAA test)
If CP = y,
PB = 3y
Now, ∆CBD ~ ∆PBQ …(AA test)
= 1 : 0.75
Hence, option (b).
Workspace:
There are 8436 steel balls, each with a radius of 1 centimetre, stacked in a pile, with 1 ball on top, 3 balls in the second layer, 6 in the third layer, 10 in the fourth, and so on. The number of horizontal layers in the pile is
- A.
34
- B.
38
- C.
36
- D.
32
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
The first layer has 1 ball.
Second layer has 1 + 2 = 3 balls
Third layer has 1 + 2 + 3 = 6 balls
∴ The nth layer of the stack would have balls
∴ Total balls in all the layers = = 8436
∴ = 8436
Only n = 36 satisfies the above equation.
Hence, option (c).
Workspace:
If the product of n positive real numbers is unity, then their sum is necessarily
- A.
a multiple of n
- B.
equal to n + 1/n
- C.
never less than n
- D.
a positive integer
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Let a1, a2, a3,…, an be n positive real numbers.
Now, a1 × a2 × a3 × … × an = 1
We know that, A.M. ≥ G.M.
a1 + a2 + a3 + … + an ≥ n × (a1 × a2 × a3 × … × an)1/n
∴ a1 + a2 + a3 + … + an ≥ n × (1)1/n
∴ a1 + a2 + a3 + … + an ≥ n
Hence, option (c).
Workspace:
If log3 2, log3 (2x − 5), log3 (2x − 7/2) are in arithmetic progression, then the value of x is equal to
- A.
5
- B.
4
- C.
2
- D.
3
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
log3 2, log3 (2x − 5), log3 (2x − 7/2) are in A.P.
∴ 2 × log3 (2x − 5) = log3 2 + log3 (2x − 7/2)
∴ log3 (2x − 5)2 = log3 [2 × (2x − 7/2)]
Let 2x = a, then we have,
(a − 5)2 = 2 × (a − 7/2)
∴ a2 − 10a + 25 = 2a − 7
∴ a2 − 12a + 32 = 0
∴ a2 − 8a − 4a + 32 = 0
(a − 8)(a − 4) = 0
a = 8 or 4
2x = 8 or 2x = 4
x = 3 and x = 2
x = 2 cannot be the answer as (2x − 5) would become negative and logarithms of negative numbers are not defined.
∴ x = 3
Hence, option (d).
Workspace:
In the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC = OB. The straight line CO is produced to meet the circle at D. If ∠ACD = y° and ∠AOD = x° such that x = ky, then the value of k is

- A.
3
- B.
2
- C.
1
- D.
None of the above
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :

Consider the figure shown above.
In ∆OBC, BC = OB
∴ ∠BOC = ∠BCO = y … (i)
Also, OB = OA = Radius of the circle
∠OBA is an exterior angle of ∆OBC.
∴ ∠OBA = ∠BOC + ∠BCO = 2y
∴ ∠OAB = ∠OBA = 2y …(ii)
∴ In ∆AOB, ∠AOB = 180 − 4y
Now, ∠AOD + ∠AOB + ∠BOC = 180°
∴ x + 180 − 4y + y = 180°
∴ x = 3y
∴ The value of k = 3
Hence, option (a).
Alternatively,
m∠ACD = 1/2 × [m(arc AD) – m(arc BM)]
∴ 2y = x – y
∴ x = 3y
Hence, option (a).
Workspace:
In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?
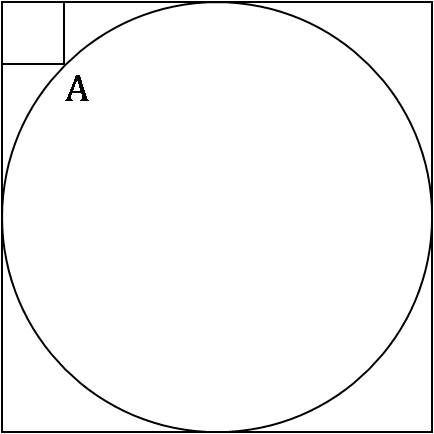
- A.
10 cm
- B.
40 cm
- C.
50 cm
- D.
None of the above
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
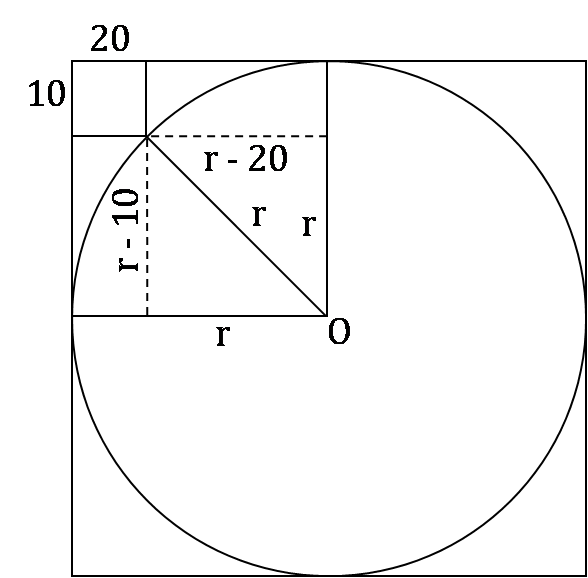
Consider the figure shown above.
(r − 20)2 + (r − 10)2 = r2
r2 + 400 − 40r + r2 + 100 − 20r = r2
r2 − 60r + 500 = 0
r2 − 50r − 10r + 500 = 0
r × (r − 50) − 10 × (r − 50) = 0
r = 50 or r = 10
But, r cannot be 10.
∴ r = 50
Hence, option (c).
Workspace:
Given that −1 ≤ v ≤ 1, −2 ≤ u ≤ −0.5 and −2 ≤ z ≤ −0.5 and w = vz/u, then which of the following is necessarily true?
- A.
−0.5 ≤ w ≤ 2
- B.
−4 ≤ w ≤ 4
- C.
−4 ≤ w ≤ 2
- D.
−2 ≤ w ≤ −0.5
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
w = vz/u
From the given range of values for u, v and z, we have,
Maximum possible value of w is 4 when v is 1, z is −2 and u is −0.5.
Also minimum value of w is −4 when v is −1, z is −2 and u is −0.5.
Hence, option (b).
Workspace:
There are 6 boxes numbered 1, 2,..., 6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 box contains a green ball and the boxes containing green balls are consecutively numbered. The total number of ways in which this can be done is
- A.
5
- B.
21
- C.
33
- D.
60
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
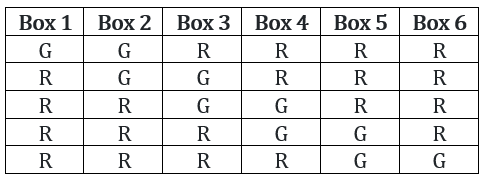
Case 1: only 1 box with green ball.
Number of possible ways = 6
Case 2: 2 boxes with green balls
Table shows that the green balls are placed in the boxes which are consecutively numbered.
Number of possible ways = 5
Similarly,
Case 3: 3 boxes with green balls
Number of possible ways = 4
Case 4: 4 boxes with green balls
Number of possible ways = 3
Case 5: 5 boxes with green balls
Number of possible ways = 2
Case 6: 6 boxes with green balls
Number of possible ways = 1
∴ Total number of ways = 6 + 5 + 4 + 3 + 2 + 1 = 21
Hence, option (b).
Workspace:
Consider the following two curves in the X-Y plane
y = x3 + x2 + 5
y = x2 + x + 5
Which of the following statements is true for −2 ≤ x ≤ 2?
- A.
The two curves intersect once
- B.
The two curves intersect twice
- C.
The two curves do not intersect
- D.
The two curves intersect thrice
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
y = x3 + x2 + 5 … (i)
y = x2 + x + 5 … (ii)
Solving (i) and (ii), we get,
x3 + x2 + 5 = x2 + x + 5
x(x2 − 1) = 0
∴ x = 0, 1, −1
∴ All three solutions for (i) and (ii) lie between −2 and 2.
∴ The two curves intersect thrice in the given range.
Hence, option (d).
Workspace:
In a certain examination paper, there are n questions. For j = 1, 2, ..., n, there are 2(n − j) students who answered j or more questions wrongly. If the total number of wrong answers is 4095, then the value of n is
- A.
12
- B.
11
- C.
10
- D.
9
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
For j = n, 2(n - n) = 1 student has answered wrongly
j = n - 1, 2[n - (n - 1)] = 2 students have answered wrongly
.
.
j = 1, 2(n - 1) students have answered wrongly
∴ 1 + 2 + ... + 2(n – 1) = 4095
The series is in G.P. with common ratio r = 2
∴ 1 × (2n − 1)/(2 − 1) = 4095
∴ 2n − 1 = 4095
∴ 2n = 4096
∴ n = 12
Hence, option (a).
Workspace:
If x, y, z are distinct positive real numbers, then would be
- A.
greater than 4
- B.
greater than 5
- C.
greater than 6
- D.
None of these
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
The given expression may be represented as
We know that, A.M. ≥ G.M.
∴ The given expression will have a minimum value of 6.
But x, y and z are distinct, so the value will always be greater than 6.
Hence, option (c).
Workspace:
A graph may be defined as a set of points connected by lines called edges. Every edge connects a pair of points. Thus, a triangle is a graph with 3 edges and 3 points. The degree of a point is the number of edges connected to it. For example, a triangle is a graph with three points of degree 2 each. Consider a graph with 12 points. It is possible to reach any point from any other point through a sequence of edges. The number of edges, e, in the graph must satisfy the condition
- A.
11 ≤ e ≤ 66
- B.
10 ≤ e ≤ 66
- C.
11 ≤ e ≤ 65
- D.
0 ≤ e ≤ 11
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
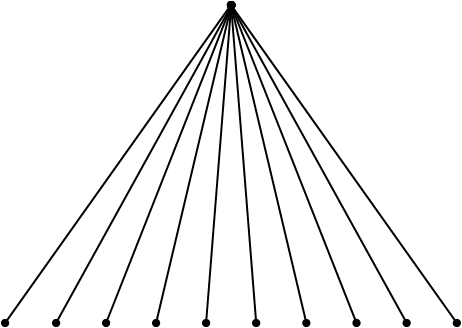
For a given triangle, any point can have 2 edges.
A graph with 12 points will have 12 − 1 = 11 edges at least as shown.
The maximum number of edges will occur when each point is connected to all the others.
∴ The first point will form 11 edges, the second will form 10 edges, the third will form 9 edges and so on.
∴ The maximum number of edges = 11 + 10 + 9 + … + 1 = 66
∴ 11 ≤ e ≤ 66
Hence, option (a).
Alternatively,
The maximum number of edges joining 12 points to each other = 12C2 = 66
To go from each point to every other point, we need at least 11 edges.
∴ 11 ≤ e ≤ 66
Hence, option (a).
Workspace:
The number of positive integers n in the range 12 ≤ n ≤ 40 such that the product (n − 1)(n − 2)...3.2.1 is not divisible by n is
- A.
5
- B.
7
- C.
13
- D.
14
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
For (n − 1)(n − 2) … 3.2.1 to not be divisible by n, n should be a prime number.
But, there are 7 prime numbers in the range 12 ≤ n ≤ 40 are 7.
The prime numbers are 13, 17, 19, 23, 29, 31, 37.
Hence, option (b).
Workspace:
Let T be the set of integers {3, 11, 19, 27, ..., 451, 459, 467} and S be a subset of T such that the sum of no two elements of S is 470. The maximum possible number of elements in S is
- A.
32
- B.
28
- C.
29
- D.
30
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
The sum of the first and last terms in T is 470.
Likewise, the sum of the second and second-last terms is also 470.
In general the sum of the nth term from the beginning and the nth term from the end is 470.
∴ Only one of each of these pairs of terms will be in S. (For instance only one of 3 and 467 can be in S)
∴ The set S can have a maximum of half of the terms in T.
The terms in T are in A.P. with a common difference of 8.
Last Term = 467 = 3 + (n − 1) × 8
∴ n = 59
∴ Total number of terms in the set T = 59
∴ there are 29 pairs of numbers in T that add up to 470 and the 59th number is 235, which occurs in the middle of the series.
∴ S will be a set with 30 terms, with 29 terms which are from the pairs adding up to 470, and 235.
Hence, option (d).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
A game consists of tossing a coin successively. There is an entry fee of Rs. 10 and an additional fee of Re. 1 for each toss of the coin. The game is considered to have ended normally when the coin turns heads on two consecutive throws. In this case the player is paid Rs. 100. Alternatively, the player can choose to terminate the game prematurely after any of the tosses. Ram has incurred a loss of Rs. 50 by playing this game. How many times did he toss the coin?
A. The game ended normally.
B. The total number of tails obtained in the game was 138.
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Let the number of tosses be x.
Total amount spent by Ram after x tosses = (10 + x × 1) = Rs. (10 + x)
We know that Ram incurs a loss of Rs. 50.
∴ We have two cases to evaluate:
i. If the game ends normally then Ram's net loss = Rs. (10 + x) − Rs. 100
ii. If he quits prematurely his loss = Rs. (10 + x)
From statement A,
Ram's net loss = (10 + x) − 100
∴ 50 = (10 + x) − 100
∴ x = 140
∴ Statement A is alone sufficient.
From statement B,
Ram gets 138 tails.
If his game ends prematurely, his loss = 10 + x = 50
∴ x = 40
This is not possibe as the number of tails > 40
∴ His game must have ended normally.
∴ 10 + x – 100 = 50
∴ x = 140
∴ Statement B is also sufficient.
Hence, option (b).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
Each packet of SOAP costs Rs. 10. Inside each packet is a gift coupon labelled with one of the letters S, O, A, and P. If a customer submits four such coupons that make up the word SOAP, the customer gets a free SOAP packet. Ms. X kept buying packet after packet of SOAP till she could get one set of coupons that formed the word SOAP. How many coupons with label P did she get in the above process?
A. The last label obtained by her was S and the total amount spent was Rs. 210.
B. The total number of vowels obtained was 18.
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
From Statement A,
Number of soaps purchased by Ms. X = = 21
Also the last label obtained by her is S.
But this is not sufficient to get the number of P's.
∴ Statement A alone is not sufficient.
From Statement B,
The number of O's and A's is 18.
But this is also not individually sufficient to arrive at the required answer.
∴ Statement B alone is not sufficient.
After combining both the statements A and B, we can conclude that 18 out of 21 coupons are O's and A's and that the 21st is an S.
∴This means that the remaining two are P's.
Hence, option (c).
Workspace:
In each question there are two statements: A and B.
Choose 1 if the question can be answered by one of the statements alone but not by the other.
Choose 2 if the question can be answered by using either statement alone.
Choose 3 if the question can be answered by using both the statements together but cannot be answered using either statement alone.
Choose 4 if the question cannot be answered even by using both the statements A and B.
If A and B run a race, then A wins by 60 seconds. If B and C run the same race, then B wins by 30 seconds. Assuming that C maintains a uniform speed, what is the time taken by C to finish the race?
A. A and C run the same race and A wins by 375 metres.
B. The length of the race is 1 km.
- A.
1
- B.
2
- C.
3
- D.
4
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
From the question, if A and C participate in a race, A will win by 90 seconds.
From statement A,
∵ A beats C by 375 m or 90 sec.
∴ C's speed =
But the length of the track is not known.
∴ Statement A is not sufficient to find the time taken by C to complete the race.
From Statement B we cannot find the speed of C.
∴ Statement B alone is not sufficient.
After combining both the statements A and B, the time taken by C to complete the race
= 240 sec
Hence, option (c).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report