CAT 2020 LRDI Slot 3 | Previous Year CAT Paper
Join our Telegram Group for CAT Preparation.
Answer the next 4 questions based on the information given below.
Sixteen patients in a hospital must undergo a blood test for a disease. It is known that exactly one of them has the disease. The hospital has only eight testing kits and has decided to pool blood samples of patients into eight vials for the tests. The patients are numbered 1 through 16, and the vials are labelled A, B, C, D, E, F, G, and H. The following table shows the vials into which each patient’s blood sample is distributed.
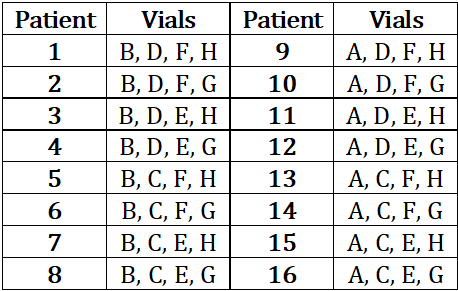
If a patient has the disease, then each vial containing his/her blood sample will test positive. If a vial tests positive, one of the patients whose blood samples were mixed in the vial has the disease. If a vial tests negative, then none of the patients whose blood samples were mixed in the vial has the disease.
Suppose vial C tests positive and vials A, E and H test negative. Which patient has the disease?
- A.
Patient 14
- B.
Patient 2
- C.
Patient 6
- D.
Patient 8
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Given, if a patient has the disease, then each vial containing his/her blood sample will test positive.
E.g., suppose patient 5 has the disease. Then vials B, C, F and H will definitely test positive.
Or if vial B tests positive, it means one of patient 1, 2, 3, 4, 5, 6, 7, 8, 9 or 10 has the disease.
If vial C tests positive, it means one of patient 5, 6, 7, 8, 13, 14, 15 or 16 has the disease.
Now, since vial A tests negative, it means that patient 9 to 16 don’t have the disease.
Now, we are left with patient 5, 6, 7 and 8 who can have the disease.
Vial E tests negative, it means patients 7 and 8 cannot have the disease.
Now, we are left with patient 5 and 6 who can have the disease.
Vial H tests negative, it means patient 5 cannot have the disease.
∴ Only patient who can have the disease is patient 6.
Hence, option (c).
Workspace:
Suppose vial A tests positive and vials D and G test negative. Which of the following vials should we test next to identify the patient with the disease?
- A.
Vial B
- B.
Vial C
- C.
Vial E
- D.
Vial H
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Since vial A tests positive one of patient 9 to 16 will have the disease.
Now, vials D and G test negative hence, patients 9, 10, 11, 12, 14 and 16 cannot have the disease.
⇒ One of patients 13 or 15 will have the disease.
To check which one of patients 13 or 15 have the disease we need to check a vial which does not have both the samples.
∴ We can check either vial E or F.
Hence, option (c).
Workspace:
Which of the following combinations of test results is NOT possible?
- A.
Vials B and D positive, vials F and H negative
- B.
Vials A and G positive, vials D and E negative
- C.
Vials A and E positive, vials C and D negative
- D.
Vial B positive, vials C, F and H negative
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Here the tests should be consistent with each other.
Checking for option (c): If vials A and E test positive, patients 11, 12, 15 or 16 will have the disease.
If vials C and D test negative, it means patients 11, 12, 15 or 16 cannot have the disease.
Since these two tests are contradictory, they cannot both be true.
Hence, option (c).
Workspace:
Suppose one of the lab assistants accidentally mixed two patients' blood samples before they were distributed to the vials. Which of the following correctly represents the set of all possible numbers of positive test results out of the eight vials?
- A.
{4,5,6,7}
- B.
{4,5,6,7,8}
- C.
{4,5}
- D.
{5,6,7,8}
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Assuming patient 1 has the disease.
Case 1: Those patient’s blood is mixed which have no common vial.
∴ Patient 1 and 16’s samples are mixed.
In this case all 8 vials i.e., A to D will have the blood of diseased patient.
⇒ All 8 vials will test positive.
Case 2: Those patient’s blood is mixed which have exactly 1 common vial.
∴ Patient 1 and 15’s samples are mixed.
In this case 7 vials i.e., A to F and H will have the blood of diseased patient.
⇒ 7 vials will test positive.
Case 3: Those patient’s blood is mixed which have exactly 2 common vials.
∴ Patient 1 and 13’s samples are mixed.
In this case 6 vials i.e., A to D, F and H will have the blood of diseased patient.
⇒ 6 vials will test positive.
Case 4: Those patient’s blood is mixed which have exactly 3 common vials.
∴ Patient 1 and 9’s samples are mixed.
In this case 5 vials i.e., A, B, D, F and H will have the blood of diseased patient.
⇒ 5 vials will test positive.
Case 5: Those patient’s blood is mixed which don’t have the disease.
∴ Patient 2 and 3’s samples are mixed.
In this case 4 vials i.e., B, D, F and H will have the blood of diseased patient.
⇒ 4 vials will test positive.
∴ Either 4, 5, 6, 7 or 8 vials can test positive.
Hence, option (b).
Workspace:
Answer the next 4 questions based on the information given.
A survey of 600 schools in India was conducted to gather information about their online teaching learning processes (OTLP). The following four facilities were studied.
F1: Own software for OTLP
F2: Trained teachers for OTLP
F3: Training materials for OTLP
F4: All students having Laptops
The following observations were summarized from the survey.
- 80 schools did not have any of the four facilities – F1, F2, F3, F4.
- 40 schools had all four facilities.
- The number of schools with only F1, only F2, only F3, and only F4 was 25, 30, 26 and 20 respectively.
- The number of schools with exactly three of the facilities was the same irrespective of which three were considered.
- 313 schools had F2.
- 26 schools had only F2 and F3 (but neither F1 nor F4).
- Among the schools having F4, 24 had only F3, and 45 had only F2.
- 162 schools had both F1 and F2.
- The number of schools having F1 was the same as the number of schools having F4.
What was the total number of schools having exactly three of the four facilities?
- A.
64
- B.
80
- C.
50
- D.
200
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Given, the number of schools with exactly three of the facilities was the same irrespective of which three were considered.
Let us assume this number to be ‘a’ for every possible combination of three OTLPs.
The following diagram can be drawn from the given information.
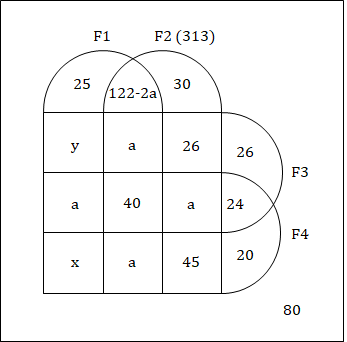
It is also given that 162 schools had F1 and F2
∴ Number of students having only F1 and F2 = 162 – (a + 40 + a) = 122 – 2a.
Total schools having F2 = 313 = 162 + 30 + 26 + a + 45
⇒ a = 50
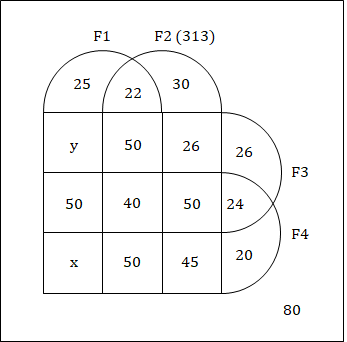
Total number of schools having F1 is equal to total number of schools having F2.
∴ (162 + 25 + y + 50 + x) = (50 + 40 + 50 + 24 + x + 50 + 45 + 20)
⇒ y = 42
Now there are a total of 600 schools
∴ 600 = 25 + 42 + 50 + x + 313 + 26 + 24 + 20 + 80
⇒ x = 20
Therefore, the complete Venn diagram is
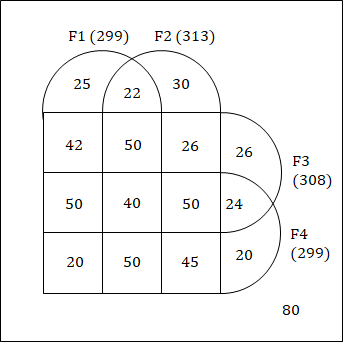
Number of schools having exactly 3 of the 4 facilities = 50 + 50 + 50 + 50 = 200
Hence, option (d).
Workspace:
What was the number of schools having facilities F2 and F4?
- A.
85
- B.
45
- C.
95
- D.
185
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Number of schools having facilities F2 and F4 = 40 + 50 + 50 + 45 = 185
Hence, option (d).
Workspace:
What was the number of schools having only facilities F1 and F3?
Answer: 42
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Number of schools having only facilities F1 and F3 = 42
Hence, 42.
Workspace:
What was the number of schools having only facilities F1 andF4?
Answer: 20
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Number of schools having only facilities F1 and F4 = 20.
Hence, 20.
Workspace:
Answer the next 4 questions based on the information given.
XYZ organization got into the business of delivering groceries to home at the beginning of the last month. They have a two-day delivery promise. However, their deliveries are unreliable. An order booked on a particular day may be delivered the next day or the day after. If the order is not delivered at the end of two days, then the order is declared as lost at the end of the second day. XYZ then does not deliver the order, but informs the customer, marks the order as lost, returns the payment and pays a penalty for non-delivery.
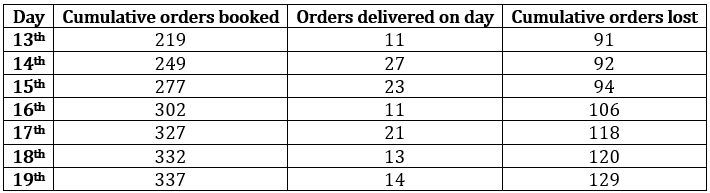
The following table provides details about the operations of XYZ for a week of the last month. The first column gives the date, the second gives the cumulative number of orders that were booked up to and including that day. The third column represents the number of orders delivered on that day. The last column gives the cumulative number of orders that were lost up to and including that day.
It is known that the numbers of orders that were booked on the 11th, 12th, and 13th of the last month that took two days to deliver were 4, 6, and 8 respectively.
Among the following days, the largest fraction of orders booked on which day was lost?
- A.
16th
- B.
13th
- C.
14th
- D.
15th
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
It is given that 4 order which were booked on 11th day were delivered on 13th day.
⇒ Out of 11 orders delivered on 13th day, 11 – 4 = 7 were booked on 12th day.
Out of total orders booked on 12th day 6 were delivered on 14th day and 1 order was lost at the end of the 14th day.
∴ Total orders booked on 12th day = 7 (delivered on 13th day) + 6 (delivered on 14th day) + 1 (lost at the end of 14th day) = 14.
Similarly,
Total orders booked on 13th day = 21 (delivered on 14th day) + 8 (delivered on 15th day) + 2 (lost at the end of 15th day) = 31.
Total orders booked on 14th day = 249 – 219 = 30.
Out of these 30 orders 23 – 8 = 15 orders were delivered on 15th day.
Also, of the orders booked on 14th day orders lost om 16th day = 12.
∴ Of the orders booked on 14th day orders delivered on 16th day = 30 – 15 – 12 = 3.
Similarly, we can make the following table for orders booked and delivered.

Fraction of orders booked on 13th day which were lost = 2/31
Fraction of orders booked on 14th day which were lost = 12/30
Fraction of orders booked on 15th day which were lost = 12/28
Fraction of orders booked on 16th day which were lost = 2/25
Largest of these fractions is 12/28 i.e., for 15th day.
Hence, option (d).
Workspace:
On which of the following days was the number of orders booked the highest?
- A.
14th
- B.
12th
- C.
15th
- D.
13th
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Highest number of orders booked is 31 on 13th day.
Hence, option (d).
Workspace:
The delivery ratio for a given day is defined as the ratio of the number of orders booked on that day which are delivered on the next day to the number of orders booked on that day which are delivered on the second day after booking. On which of the following days, was the delivery ratio the highest?
- A.
16th
- B.
15th
- C.
14th
- D.
13th
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Delivery ratio for 13th day = 21/8
Delivery ratio for 14th day = 15/3
Delivery ratio for 15th day = 8/8
Delivery ratio for 16th day = 13/10
Highest of these delivery ratios is 15/3 = 5 for 14th day.
Hence, option (c).
Workspace:
The average time taken to deliver orders booked on a particular day is computed as follows. Let the number of orders delivered the next day be x and the number of orders delivered the day after be y. Then the average time to deliver order is (x+2y)/(x+y). On which of the following days was the average time taken to deliver orders booked the least?
- A.
13th
- B.
15th
- C.
16th
- D.
14th
Answer: Option D
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to the first question of this set.
Average time taken for 13th day = = 1.27
Average time taken for 14th day = = 1.16
Average time taken for 15th day = = 1.5
Average time taken for 16th day = = 1.43
Least of these average times is 1.16 for 14th day.
Hence, option (d).
Workspace:
Answer the next 4 questions based on the information given.
The Hi-Lo game is a four-player game played in six rounds. In every round, each player chooses to bid Hi or Lo. The bids are made simultaneously. If all four bid Hi, then all four lose1 point each. If three players bid Hi and one bids Lo, then the players bidding Hi gain 1 point each and the player bidding Lo loses 3 points. If two players bid Hi and two bid Lo, then the players bidding Hi gain 2 points each and the players bidding Lo lose 2 points each. If one player bids Hi and three bid Lo, then the player bidding Hi gains 3 points and the players bidding Lo lose 1 point each. If all four bid Lo, then all four gain 1 point each.
Four players Arun, Bankim, Charu, and Dipak played the Hi-Lo game. The following facts are known about their game:
- At the end of three rounds, Arun had scored 6 points, Dipak had scored 2 points, Bankim and Charu had scored -2 points each.
- At the end of six rounds, Arun had scored 7 points, Bankim and Dipak had scored -1 point each, and Charu had scored -5 points.
- Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
- In exactly two out of the six rounds, Arun was the only player who bid Hi.
What were the bids by Arun, Bankim, Charu and Dipak, respectively in the first round?
- A.
Hi, Lo, Lo, Lo
- B.
Lo, Lo, Lo, Hi
- C.
Hi, Lo, Lo, Hi
- D.
Hi, Hi, Lo, Lo
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Points scored in a round has the following possibilities:
H H H H: (-1, -1, -1, -1); Total -4
H H H L: (1, 1, 1, -3); Total 0
H H L L: (2, 2, -2, -2); Total 0
H L L L: (3, -1, -1, -1); Total 0
L L L L: (1, 1, 1, 1); Total 4
Total points scored in a round can be -4, 0 or 4.
We can make the following table from the data given.

Net score after first 3 rounds is 6 – 2 – 2 + 2 = 4.
This could have happened if the total score in first three rounds was {4, 4, -4} or {4, 0, 0} in any order.
∴ In one of the first 3 rounds the net score has to be 4. This is only possible when all of them bid Lo and score 1 point each.
Now, Arun scored total 6 points in first 3 rounds. Also, he scores 1 in one of the first 3 rounds. This is possible if he scores {3, 2, 1} in any order in the first 3 rounds.
For Arun to score 3 in a round he will have to bid Hi and other will bid Lo. Other 3 will score -1 each.
For Arun to score 2 in a round he will have to bid Hi along with one other and the remaining two will bid Lo. Scores of other 3 will be {2, -2, -2} in any order.
Dipak’s score in two of the rounds is 1 and -1. His net score in 3 rounds is 2. Hence, Dipak scores 2 in one of the first three rounds.
Also, Dipak’s score in the third round was less than his score in the first round but was more than his score in the second round.
∴ We can make the following table for the first 3 rounds.

Net score in last 3 rounds is 1 + 1 – 3 - 3 = -4.
This could have happened if the total score in last three rounds was {4, -4, -4} or {-4, 0, 0} in any order.
∴ In one of the last 3 rounds the net score has to be -4. This is only possible when all of them bid Hi and score -1 point each.
In exactly two out of the six rounds, Arun was the only player who bid Hi i.e., Arun scores 3 in exactly 2 of the six rounds.
∴ Arun scored 3 in one of the last 3 rounds. Also, his net score in last 3 rounds is 1. Hence, he scores -1 and -1 in 2 of the last 3 rounds.
∴ We can make the following table for the all 6 rounds.

In first round Arun, Bankim, Charu and Dipak bid Hi, Lo, Lo and Hi.
Hence, option (c).
Workspace:
In how many rounds did Arun bid Hi?
Answer: 4
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Arun bid Hi in 4 rounds.
Hence, 4.
Workspace:
In how many rounds did Bankim bid Lo?
Answer: 4
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Bankim bid Lo in 4 rounds.
Hence, 4.
Workspace:
In how many rounds did all four players make identical bids?
Answer: 2
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
All 4 made identical bids in 2 of these 6 rounds.
Hence, 2.
Workspace:
In how many rounds did Dipak gain exactly 1 point?
Answer: 1
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Dipak gained exactly 1 point in only 1 round (i.e., Round 3).
Hence, 1.
Workspace:
In which of the following rounds, was Arun DEFINITELY the only player to bid Hi?
- A.
First
- B.
Second
- C.
Third
- D.
Fourth
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Arun was definitely the only player to bid Hi in round 2.
Hence, option (b).
Workspace:
Answer the next 4 questions based on the information given.
A farmer had a rectangular land containing 205 trees. He distributed that land among his four daughters – Abha, Bina, Chitra and Dipti by dividing the land into twelve plots along three rows (X,Y,Z) and four Columns (1,2,3,4) as shown in the figure below:

The plots in rows X, Y, Z contained mango, teak and pine trees respectively. Each plot had trees in non-zero multiples of 3 or 4 and none of the plots had the same number of trees. Each daughter got an even number of plots. In the figure, the number mentioned in top left corner of a plot is the number of trees in that plot, while the letter in the bottom right corner is the first letter of the name of the daughter who got that plot (For example, Abha got the plot in row Y and column 1 containing 21 trees). Some information in the figure got erased, but the following is known:
- Abha got 20 trees more than Chitra but 6 trees less than Dipti.
- The largest number of trees in a plot was 32, but it was not with Abha.
- The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4.
- Both Abha and Bina got a higher number of plots than Dipti.
- Only Bina, Chitra and Dipti got corner plots.
- Dipti got two adjoining plots in the same row.
- Bina was the only one who got a plot in each row and each column.
- Chitra and Dipti did not get plots which were adjacent to each other (either in row / column /diagonal).
- The number of mango trees was double the number of teak trees.
How many mango trees were there in total?
- A.
49
- B.
126
- C.
98
- D.
84
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
The number of teak trees in Column 3 was double of that in Column 2 but was half of that in Column 4. The number of mango trees was double the number of teak trees.
Dipti got two adjoining plots in the same row. Chitra and Dipti did not get plots which were adjacent to each other (either in row / column /diagonal).
∴ Dipti must have got adjacent plots in row X in column 3 and 4.
Bina got a plot in each row and column. Hence, Bina gets last plot in row Z last column.
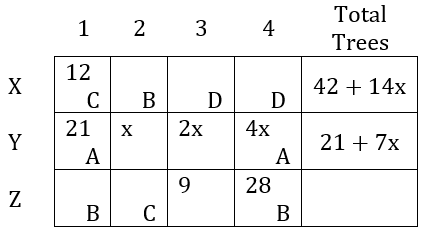
Number of plots so far: A = 2, B = 3, C = 2 and D = 2
Since each daughter gets even number of plots and Abha and Bina got more plots than D.
∴ Bina gets one more plot in 2nd column in row X and Abha will get 2 more plots.

Now, highest trees in a plot is 32 but this plot doesn’t belong to Abha hence, 4x < 32
⇒ x < 8
Also, x should be a multiple of 3 or 4. Hence, x can be 3, 4 or 6.
x cannot be 3 as 4x = 12 but all plots need to have different number of trees.
Also, x cannot be 6 as 2x = 12 but all plots need to have different number of trees.
∴ x = 4.

Abha got 20 trees more than Chitra but 6 trees less than Dipti.
Abha gets total 21 + 4 + 9 + 16 = 50 tress.
∴ Chitra gets 30 trees
& Dipti gets 56 trees
& Bina will have = 205 – 50 – 30 – 56 = 69 trees
Since Dipti has 56 trees, in the first row B will have 98 – 56 – 12 = 30 trees.
Trees for B = 69 = 30 + 8 + 28 + (trees in row Z first column)
∴ Trees for B in row Z first column = 3
Number of trees for C in row Z = 58 – 3 – 9 – 28 = 18.
Now, highest number of trees in a plot is 32, this must be with D in row X.
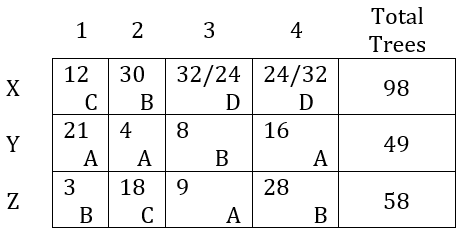
Total number of mango trees is 98.
Hence, option (c).
Workspace:
Which of the following is the correct sequence of trees received by Abha, Bina, Chitra and Dipti in that order?
- A.
44, 87, 24, 50
- B.
50, 69, 30, 56
- C.
60, 39, 40, 66
- D.
54, 57, 34, 60
Answer: Option B
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Trees received by A = 50, B = 69, C = 30 and D = 56.
Hence, option (b).
Workspace:
How many pine trees did Chitra receive?
- A.
18
- B.
15
- C.
30
- D.
21
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Chitra received 18 pine trees. (Row Z, column 2)
Hence, option (a).
Workspace:
Who got the plot with the smallest number of trees and how many trees did that plot have?
- A.
Dipti, 6 trees
- B.
Bina, 4 trees
- C.
Bina, 3 trees
- D.
Abha, 4 trees
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Bina got the plot with the smallest number of trees, which had 3 trees. (Row Z, column 1)
Hence, option (c).
Workspace:
Which of the following statements is NOT true?
- A.
Abha got 41 teak trees.
- B.
Chitra got 12 mango trees.
- C.
Bina got 32 pine trees.
- D.
Dipti got 56 mango trees.
Answer: Option C
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Bina got 31 pine trees.
Hence, option (c).
Workspace:
Which column had the highest number of trees?
- A.
4
- B.
2
- C.
3
- D.
Cannot be determined
Answer: Option A
Join our Telegram Group for CAT Preparation.
Explanation :
Consider the solution to first question of this set.
Column 4 will have the highest number of trees.
Hence, option (a).
Workspace:
Feedback
Help us build a Free and Comprehensive Preparation portal for various competitive exams by providing us your valuable feedback about Apti4All and how it can be improved.
 Solution
Solution Discuss
Discuss Report
Report