CAT 2023 QA Slot 1 | Previous Year CAT Paper

Answer: Option C

Video Explanation

Explanation :

Single-digit such numbers = 9

2-digit such numbers: __ __
Ten’s digit can be filled in 9 ways (i.e., 1, 2, 3, …, 9)
Unit’s digit can be filled in 9 ways (i.e., any of the 10 single digits except the one at ten’s place)
⇒ Total such 2-digit numbers = 9 × 9 = 81

3-digit such numbers: __ __ __
Hundred’s digit can be filled in 9 ways (i.e., 1, 2, 3, …, 9)
Ten’s digit can be filled in 9 ways (i.e., any of the 10 single digits except the one at hundred’s place)
Unit’s digit can be filled in 8 ways (i.e., any of the 10 single digits except the ones at hundred’s and ten’s place)
⇒ Total such 3-digit numbers = 9 × 9 × 8 = 648

∴ Total such numbers = 9 + 81 + 648 = 738.

Hence, option (c).

Answer: 2

Video Explanation

Explanation :

​​​​​​​

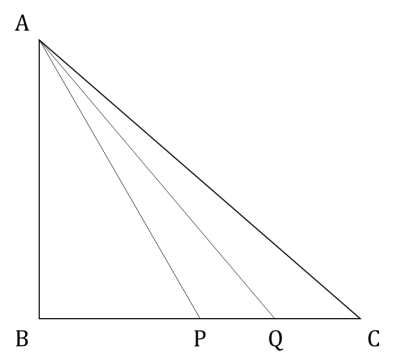
Given, AB = 5 and BC = 12

Area of ∆ABP = ½ × AB × BP = 2.5 × BP    …(1)
Area of ∆ABQ = ½ × AB × BQ = 2.5 × BQ    …(2)
Area of ∆ABC = ½ × AB × BC = 2.5 × BC    …(3)

Given, (3) = 1.5 × (1)
⇒ 2.5 BC = 1.5 × 2.5 × BP
⇒ BC = 1.5 × BP
⇒ 12 = 1.5 × BP
⇒ BP = 8

Also, Areas of ∆ABP, ∆ABQ and ABC are in arithmetic progression.
⇒ 2 × (2) = (1) + (3)
⇒ 2 × 2.5 × BQ = 2.5 × BP + 2.5 × BC
⇒ 2BQ = BP + BC
⇒ 2BQ = 8 + 12
⇒ BQ = 10

∴ PQ = BQ – BP = 10 – 8 = 2

Hence, 2.

Concept:

Area of a Triangle

Arithmetic Progression

Answer: Option D

Video Explanation

Explanation :

Let the initial quantity of coffee in the jar be 100 kg and r kg is replaced each time.

Since r kg out of 100 kg is removed, fraction of coffee removed = r/100
∴ fraction of coffee remaining = $\left(1-\frac{\mathrm{r}}{100}\right)$

⇒ Quantity of coffee remaining after first replacement = 100 × $\left(1-\frac{\mathrm{r}}{100}\right)$
And quantity of cocoa after first replacement = r kgs.

⇒ Similarly, quantity of coffee remaining after second replacement = 100 × ${\left(1-\frac{\mathrm{r}}{100}\right)}^2$

Now, after 2nd replacement coffee and cocoa are in the ratio of 16 : 9
⇒ Quantity of coffee left after 2nd replacement = $\frac{16}{16+9}$ × 100 = 64 kg

⇒ 100 × ${\left(1-\frac{\mathrm{r}}{100}\right)}^2$ = 64

⇒ ${\left(1-\frac{\mathrm{r}}{100}\right)}^2$= $\frac{64}{100}$

⇒ $\left(1-\frac{\mathrm{r}}{100}\right)$ = $\frac{8}{10}$ = $\frac{4}{5}$

⇒ r = 20 kg

∴ 20 kg of cocoa is added after 1st replacement.
Also, quantity of cocoa after 2nd replacement = 100 – 64 = 36 kgs

⇒ Required ratio = 20 : 36 = 5 : 9.

Hence, option (d).

Concept:

Removal & Replacement

Answer: Option D

Video Explanation

Explanation :

Total distance travelled at the end of the trip = 26,862.
This includes the distance which car had travelled before the trip and the distance it travels in the 8 hours of the trip.

To maximize speed in 8 hours, we need to maximize distance travelled in 8 hours.
∴ We need to minimize the distance travelled by car before the trip starts, hence we need to minimize x.

Since Brishti drove at less than 110 kmph, hence she must have travelled less than 110 × 8 = 880 kms in the last 8 hours.

∴ She must have travelled more than 26862 – 880 = 25,982 kms before the last 8 hours.
⇒ x > 25,982 and it has to be a palindrome.

Least palindrome greater than 25,982 is 26062.

∴ Car travelled at least 26062 kms before the trip, hence maximum distance travelled during the trip = 26862 – 26062 = 800 kms.

⇒ Maximum average speed for the trip = 800/8 = 100 kmph.

Hence, option (d).

Concept:

Average Speed

Palindromic Number

Answer: Option A

Video Explanation

Explanation :

Given, x² + (x – 2y - 1)² = -4y(x + y)

⇒ x² + (x – 2y - 1)² = -4yx - 4y² 

⇒ x² + 4yx + 4y² + (x – 2y - 1)² = 0

⇒ (x² + 2 × x × 2y + (2y)²) + (x – 2y - 1)² = 0

⇒ (x + 2y)² + (x – 2y - 1)² = 0

Sum of squares of two number can be 0 only when both the numbers are 0.

∴ x + 2y = 0 and x – 2y – 1 = 0

⇒ x – 2y = 1

Hence, option (a).

Answer: 3

Video Explanation

Explanation :

Case 1: x ≥ 0 ⇒ |x| = x
∴ 2 × x × (x² + 1) = 5x²
⇒ 2x(x² + 1) = 5x² 
⇒ 2x(x² + 1) - 5x² = 0
⇒ x[2(x² + 1) - 5x] = 0
⇒ x(2x² – 5x + 2) = 0 
⇒ x(2x² – 4x - x + 2) = 0 
⇒ x[2x(x – 2) - (x - 2)] = 0 
⇒ x(2x - 1)(x - 2) = 0
⇒ x = 0 or ½ or 2.
We need only integral solutions hence acceptable answers are 0 and 2.

Case 2: x < 0 ⇒ |x| = -x
∴ 2 × -x × (x² + 1) = 5x²
⇒ -2x(x² + 1) = 5x² 
⇒ 2x(x² + 1) + 5x² = 0
⇒ x[2(x² + 1) + 5x] = 0
⇒ x(2x² + 5x + 2) = 0
⇒ x(2x² + 4x + x + 2) = 0
⇒ x[(2x(x + 2) + (x + 2)] = 0
⇒ x(2x + 1)(x + 2) = 0
⇒ x = 0 or -1/2 or -2
We need only integral solutions hence acceptable answers are 0 and -2.

∴ Acceptable integral solutions are -2, 0 and 2, i.e., 3 integral solutions.

Hence, 3.

Concept:

Solving a Quadratic Equation

Answer: Option D

Video Explanation

Explanation :

Let the selling price be Rs. x

Cost price of item sold to A = x/1.2
Cost price of item sold to B = x/0.9

To make calculations easier assume x = 108 (LCM of 12 and 9) 

∴ Cost price of item sold to A = x/1.2 = 90
∴ Cost price of item sold to B = x/0.9 = 120

Now, selling price is increased such that a profit of 10% is made for item B.
⇒ New selling price = 120 × 1.1 = Rs. 132

∴ For A, cost price = Rs. 90 and selling price = Rs. 132.
⇒ % profit for A = $\frac{(132-90)}{90}$ × 100% = 46.66% ≈ 47%.

Hence, option (d).

Concept:

Profit & Loss

Answer: Option B

Video Explanation

Explanation :

The angle between the two hands at h hours and m minutes = $\left|30\mathrm{h}-\frac{11}{2}\mathrm{m}\right|$

∴ Angle at 8:48 am = $\left|30\times 8-\frac{11}{2}\times 48\right|$ = |240 - 264| = 24°.

Now, the angle between the two hands should increase by 50% i.e., 12°.

Relative speed of the two hands = 6 – ½ = 11/2°/min.

∴ Time taken for angle to increase 12° = $\frac{12}{11/2}$ = $\frac{24}{11}$ minutes.

Hence, option (b).
 

Concept:

Angle between hands of a Clock.

Answer: 6

Video Explanation

Explanation :

α and β be two distinct root of 2x² – 6x + k = 0,
∴ α + β = -(-6)/2 = 3
And, α × β = k/2 = k/2

Now, 3 and k are the roots of the equation x² + px + p = 0.
∴ Sum of the roots = 3 + k/2 = -(p)/1 = -p    …(1)
∴ Product of the roots = 3 × k/2 = (p)/1 = p    …(2)

(1) + (2)
⇒ 3 + k/2 + 3k/2 = p – p = 0
⇒ k = -3/2

⇒ p = -9/4    [from (2)]

Now, we need to find 8(k - p)
= $8\left(\frac{-3}{2}-\frac{-9}{4}\right)$
= $8\left(\frac{3}{4}\right)$
= 6

Hence, 6.

Concept:

Sum & Product of roots of a Quadratic Equation

Answer: 20808

Video Explanation

Explanation :

Half yearly interest = 4/2 = 2%.

Amount Anil gets after 6 years = 22000 × ${\left(1+\frac{2}{100}\right)}^{6\times 2}$

Let the amount which Sunil invests = S.
Amount Sunil gets after 5 years = S × ${\left(1+\frac{2}{100}\right)}^{5\times 2}$

Sunil invests this amount for 6^th year at 10% p.a.
∴ Amount Sunil gets at the end of 6 years = S × ${\left(1+\frac{2}{100}\right)}^{5\times 2}$ × 1.1

⇒ S × ${\left(1+\frac{2}{100}\right)}^{5\times 2}$ × 1.1 =  22000 × ${\left(1+\frac{2}{100}\right)}^{6\times 2}$

⇒ S × 1.1 = 22000 × ${\left(1+\frac{2}{100}\right)}^2$

⇒ S = 20000 × (1.02)² 

⇒ S = 20000 × 1.0404 = 20,808.

Hence, 20808.

Concept:

Compounding Multiple Times in a Year

Answer: 972

Video Explanation

Explanation :

After meeting they take 6 and 24 hours to reach opposite end.
∴ Time taken to meet = $\sqrt{6\times 24}$ = √144 = 12 hours.

⇒ X takes a total of 12 + 6 = 18 hours to reach from A to B.

∴ Distance between A and B = distance travelled by X in 18 hours = 18 × 54 = 972 kms.

Hence, 972.

Concept:

Time taken to reach other end after meeting

Answer: Option D

Video Explanation

Explanation :

Given, log_x (x² + 12) = 4
⇒ x² + 12 = x⁴ 
⇒ a + 12 = a²     [Take x² = a]
⇒ a² – a – 12 = 0
⇒ (a – 4)(a + 3) = 0
⇒ a = -3 or 4.        [a = x² cannot be negative hence -3 is rejected]
⇒ x² = 4 
⇒ x = ± 2        [x = -2 is rejected as log is not defined for negative numbers]
⇒ x = 2

Also, 3log_y x = 1
⇒ 3log_y 2 = 1
⇒ log_y 2³ = 1
⇒ 2³ = y¹ 
⇒ y = 8

∴ x + y = 2 + 8 = 10

Hence, option (d).

Concept:

Logarithm Properties

Answer: 19

Video Explanation

Explanation :

Number of micro-organisms on day 1 = 2

Number of micro-organisms on day 2 = 2 × 2 + 3
                                                                            = 2² + 3
Number of micro-organisms on day 3 = 2 × (2² + 3) + 3
                                                                            = 2³ + 3 × (2 + 1)
Number of micro-organisms on day 4 = 2 × (2³ + 3 × (2 + 1)) + 3
                                                                            = 2⁴ + 3 × (2² + 2 + 1)
Number of micro-organisms on day 5 = 2 × (2⁴ + 3 × (2² + 2 + 1)) + 3
                                                                            = 2⁵ + 3 × (2³ + 2² + 2 + 1)

∴ Number of micro-organisms at the end of day n = 2ⁿ + 3 × (2^n-2 + … + 2² + 2 + 1)
                                                                            = 2 × 2^n-1 + 3 × (2^n-1 - 1)
                                                                            = 5 × 2^n-1 - 3

Now, 5 × 2^n-1 - 3 ≥ 10,00,000
⇒ 2^n-1 ≥ 2,00,000 + 3/5

The least value of (n - 1) satisfying above inequality is 18.
⇒ n - 1 = 18
⇒ n = 19

Hence, 19.

Answer: Option C

Video Explanation

Explanation :

168 = 2³ × 21 = 2³ × 3 × 7
1134 = 2 × 567 = 2 × 3⁴ × 7 

Now (1134)ⁿ = 2ⁿ × 34ⁿ × 7ⁿ 
Since 168 (2³ × 3 × 7) completely divides 1134_n (2ⁿ × 34ⁿ × 7ⁿ)
⇒ Power of 2 in 1134_n ≥ Power of 2 in 168
⇒ n ≥ 3
Similarly, we can check for power of 3 and power of 7 and we get the least value of n = 3.

Now (168)^m = 2^3m × 3^m × 7^m 
Since 1134ⁿ (2ⁿ × 3⁴ⁿ × 7ⁿ = 2³ × 3¹² × 7³) completely divides 168m (2^3m × 3^m × 7^m)
⇒ Power of 3 in 168^m ≥ Power of 3 in 1134ⁿ 
⇒ m ≥ 12
Similarly, we can check for power of 2 and power of 7 and we get the least value of m = 12.

∴ n + m = 3 + 12 = 15

Hence, option (c).

Concept:

Factors

Answer: 2

Video Explanation

Explanation :

Let p and q be the other two real roots of the given cubic equation.

Product of the three roots of the given cubic equation = - $\frac{2}{1}$ = -2 × p × q
⇒ q = 1/p

∴ The three roots are -2, p and 1/p

Sum of the three roots of the given cubic equation = - $\frac{2\mathrm{r}+1}{1}$ = -2 + p + $\frac{1}{\mathrm{p}}$
⇒ p + $\frac{1}{\mathrm{p}}$ = -2r + 1

We know than sum of a number and its reciprocal is either less than or equal to - 2 or greater than or equal to 2.

⇒ 2 ≤ p + $\frac{1}{\mathrm{p}}$ ≤ -2

⇒ 2 ≤ -2r + 1 ≤ -2

⇒ 1 ≤ -2r ≤ -3

⇒ -1/2 ≥ r ≥ 3/2

∴ Least non-negative integral value of r is 2.

Hence, 2.

Concept:

Sum & Product of the roots of a Polynomial Equation

Answer: Option A

Video Explanation

Explanation :

Let the initial salaries of A, B and C be 5x, 6x and 7x respectively.

Salary of A increases by 20% and then by 40%.
∴ Salary of A after 2 years = 5x × 1.2 × 1.4 = 8.4x

Salary of C increases by 20% and then by 25%.
∴ Salary of C after 2 years = 7x × 1.2 × 1.25 = 10.5x

At the end of 2 years, B's salary is average of all three, hence B's salary will also be average of salaries of A and C.
⇒ Salary of B after 2 years = (8.4x + 10.5x)/2 = 9.45

Let the % increase in B's salary be P% in 2^nd year. Increase in first year is 25%.
⇒ 9.45x = 6x × 1.25 × (1 + P/100)
⇒ (1 + P/100) = 9.45/7.5 = 1.26
⇒ P = 26%

Hence, option (a).

Concept: Percentage Change

Concept:

Successive % Change

Answer: Option C

Video Explanation

Explanation :

Let the average marks of a boy and girl be b and g respectively.

Given, (4g + 6b)/10 = 24
⇒ 4g + 6b = 240
⇒ 2g + 3b = 120   ...(1)

Also, b ≤ g ≤ 2b
⇒ 2b ≤ 2g ≤ 4b   
⇒ 5b ≤ 2g + 3b ≤ 7b  ...(2)

From (1) & (2), we get
​​​​​​​5b ≤ 120 ≤ 7b
⇒ b ≤ 24 and b ≤ 17(1/7)   ...(3)

Now we need to find integral values of 2g + 6b
= 2g + 3b + 3b
= 120 + 3b
120 + 3 × 120/7 ≤ 120 + 3b ≤ 120 + 3 × 24   ...from (3)
⇒ 171.42 ≤ 120 + 3b ≤ 192

∴ Integral possible values of 2g + 6b are from 172 till 192 i.e., 21 possible integral values.

Hence, option (c).

Answer: 27

Video Explanation

Explanation :

Let the time taken by A and K to complete a work is x and 2x days respectively.

Work done in a day is the efficiency of a person. 

Hence, if efficiencies of A, S and K are in Harmonic Progression, time taken by them to finish a work will be in Arithmetic Progression.

∴ Time taken by S alone is arithmetic mean of time taken by A and K alone.
⇒ Time taken by S alone = (x + 2x)/2 = 1.5x

Using unitary method
⇒ 1 = $\frac{1}{\mathrm{x}}\times 4$ + $\frac{1}{1.5\mathrm{x}}\times 9$ + $\frac{1}{2\mathrm{x}}\times 16$

⇒ x = 4 + 6 + 8

⇒ x = 18

∴ S will take 1.5 × 18 = 27 days to finish the job alone.

Hence, 27.

Concept:

Harmonic Progression

Time & Work

Answer: Option A

Video Explanation

Explanation :

Given, $\sqrt{5x+9}$ + $\sqrt{5x-9}$ = 6 + 3√2

⇒ $\sqrt{5x+9}$ + $\sqrt{5x-9}$ = √36 + √18

∴ $\sqrt{5x+9}$= √36 and $\sqrt{5x-9}$= √18

⇒ 5x + 9 = 36 and 5x - 9 = 18

⇒ 5x = 27

⇒ 10x = 54

⇒ 10x + 9 = 63

⇒ $\sqrt{10x+9}$ = √63

⇒ $\sqrt{10x+9}$ = 3√7

Hence, option (a).

Answer: Option B

Video Explanation

Explanation :

Given, $\frac{2}{\sqrt{\mathrm{y}}+\sqrt{\mathrm{z}}}$ = $\frac{1}{\sqrt{\mathrm{x}}+\sqrt{\mathrm{z}}}$ + $\frac{1}{\sqrt{\mathrm{x}}+\sqrt{y}}$

⇒ $\frac{2}{\sqrt{\mathrm{y}}+\sqrt{\mathrm{z}}}$ = $\frac{\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}}+\sqrt{\mathrm{x}}+\sqrt{\mathrm{z}}}{(\sqrt{\mathrm{x}}+\sqrt{\mathrm{z}})(\sqrt{\mathrm{x}}+\sqrt{\mathrm{y}})}$

⇒ 2(√x + √z)(√x + √y) = (2√x + √y + √z)(√y + √z)

⇒ 2x + 2√xy + 2√zx + 2√zy = 2√xy + 2√xz + y + √yz + zy + z

⇒ 2x = y + z

∴ y, x and z are in Arithmetic Progression

Hence, option (b).

Concept:

Arithmetic Progression

Answer: Option C

Video Explanation

Explanation :

Let C be the circle x² + y² + 4x - 6y - 3 = 0 and L be the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60 degree. Then, the point at which L touches the line x = 6 is?

Given, x² + y² + 4x - 6y - 3 = 0
⇒ x² + 4x + 4 + y² - 6y + 9 - 3 - 4 - 9 = 0 [Adding and Subtracting 4 and 9]
⇒ (x + 2)² + (y - 3)² = 16
⇒ (x + 2)² + (y - 3)² = 4² 

This represents the equation of a circle with radius = 4 units and center (O) at (-2, 3).

Point L lies on line x = 6, hence x-coordinate of L is 6. Let y-coordinate of L be 'y'.

Let P be the point where tangent from L touches the given circle.

​​​​​​​

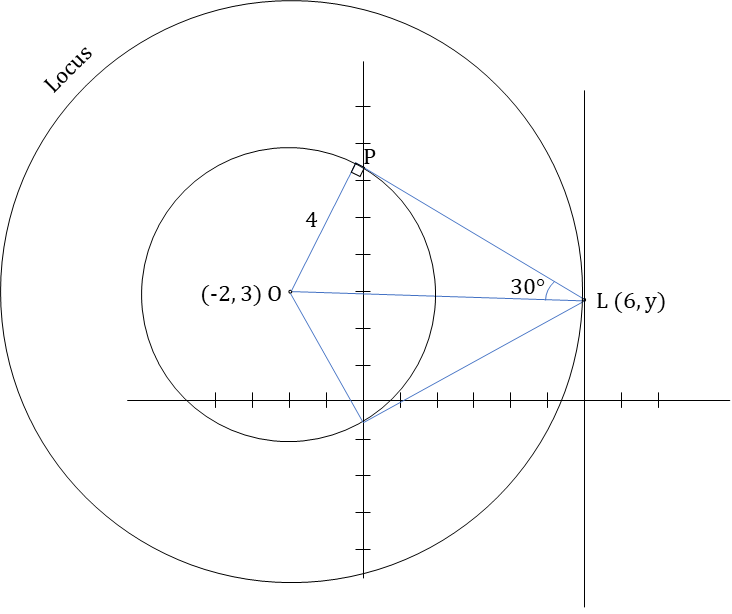
∆LOP is a 30-60-90° triangle.
⇒ OL = 2 × OP = 8

∴ OL = 8 = $\sqrt{(6 - {(-2))}^2+{(3-\mathrm{y})}^2}$
⇒ 64 = (8)² + (3 - y)² 
⇒ y = 3

∴ Coordinate of L = (6, 3)

Hence, option (c).

Note: A locus of points is a set of points that all satisfy some given condition or property.
Here L is the locus of the point of intersection of a pair of tangents to C with the angle between the two tangents equal to 60 degree. Hence, L will be a circle bigger than the original circle as shown. Tangents drawn from any point on this circle to the smaller circle will make an angle of 60 degree.

Concept:

Equation of a Circle

Answer: Option D

Video Explanation

Explanation :

​​​​​​​​​​​​​​

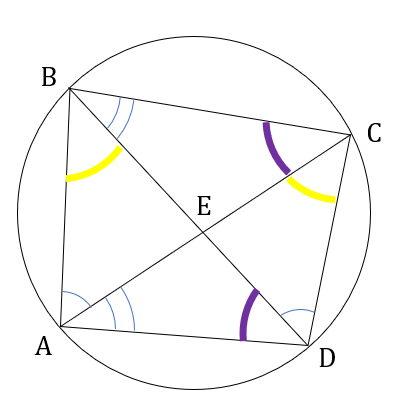
∠DAC = ∠DBC [angle subtended in same segment by same chord are equal]
Similarly,
∠ADB = ∠ACB
∠CDB = ∠CAB
∠ACD = ∠ABD

∆AED is similar to ∆BEC
[∠DAC = ∠DBC and ∠ADB = ∠ACB]
∴ $\frac{\mathrm{ED}}{\mathrm{EC}}$ = $\frac{\mathrm{AD}}{\mathrm{BC}}$ = $\frac{4}{5}$   ...(1)

∆AEB is similar to ∆DEC
[∠CDB = ∠CAB and ∠ACD = ∠ABD]
∴ $\frac{\mathrm{AE}}{\mathrm{ED}}$ = $\frac{\mathrm{AB}}{\mathrm{CD}}$ = $\frac{2}{1}$   ...(2)

(1) × (2)
⇒$\frac{\mathrm{ED}}{\mathrm{EC}}\times \frac{\mathrm{AE}}{\mathrm{ED}}$ = $\frac{4}{5}\times \frac{2}{1}$ = $\frac{8}{5}$

Hence, option (d).

Concept:

Angle subtended in same segment of a circle by same chord are equal